
已知△OFQ的面積為S,且![]() ·
·![]() =1.
=1.
(1)若![]() <S<2,求向量
<S<2,求向量![]() 與
與![]() 的夾角q 的取值范圍;
的夾角q 的取值范圍;
(2)設![]() =c(c≥2),S=
=c(c≥2),S=![]() c,若以O為中心,F為焦點的橢圓經過點Q,當|
c,若以O為中心,F為焦點的橢圓經過點Q,當|![]() |取得最小值時,求此橢圓的方程.
|取得最小值時,求此橢圓的方程.
解 (1)由已知,得 且| ∴ ∴ 1<tanq <4,則 (2)以O為原點, 設橢圓方程為 ∵ △OFG的面積為 ∴ | 又由
=( =1, 得 | = 當且僅當c=2時,| 由此可得 故橢圓方程為 點評 有關長度、角度和垂直的問題都可以用向量的數量積處理.
|


科目:高中數學 來源: 題型:
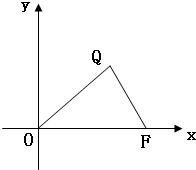 已知△OFQ的面積為2
已知△OFQ的面積為2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知△OFQ的面積為S,且
如圖,已知△OFQ的面積為S,且| OF |
| FQ |
| 1 |
| 2 |
| ||
| 2 |
| OF |
| FQ |
| OF |
| 3 |
| 4 |
| OQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
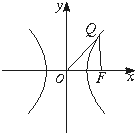 已知△OFQ的面積為2
已知△OFQ的面積為2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知△OFQ的面積為2
已知△OFQ的面積為2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2007•天津一模)已知△OFQ的面積為2
(2007•天津一模)已知△OFQ的面積為2| 6 |
| OF |
| FQ |
| 2 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com