
【題目】已知函數f(x)=ax2+bx﹣a+2
(1)若關于x的不等式f(x)>0的解集是(﹣1,3),求實數a,b的值;
(2)若b=2,a>0,解關于x的不等式f(x)>0.
【答案】
(1)解:不等式f(x)>0的解集是(﹣1,3)
∴﹣1,3是方程ax2+bx﹣a+2=0的兩根,
∴可得 ![]() ,解之得
,解之得 ![]()
(2)解:當b=2時,f(x)=ax2+2x﹣a+2=(x+1)(ax﹣a+2),
∵a>0,∴ ![]()
①若 ![]() ,即a=1,解集為{x|x≠﹣1}.
,即a=1,解集為{x|x≠﹣1}.
②若 ![]() ,即0<a<1,解集為
,即0<a<1,解集為 ![]() .
.
③若 ![]() ,即a>1,解集為
,即a>1,解集為 ![]()
【解析】(1)根據題意并結合一元二次不等式與一元二方程的關系,可得方程ax2+bx﹣a+2=0的兩根分別為﹣1和3,由此建立關于a、b的方程組并解之,即可得到實數a、b的值;(2)不等式可化成(x+1)(ax﹣a+2)>0,由此討論﹣1與 ![]() 的大小關系,分3種情形加以討論,即可得到所求不等式的解集.
的大小關系,分3種情形加以討論,即可得到所求不等式的解集.


科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別為內角A,B,C的對邊,且2sin Acos C=2sin B-sin C.
(1)求A的大小;
(2)在銳角三角形ABC中, ![]() ,求c+b的取值范圍.
,求c+b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】宿州某中學N名教師參加“低碳節能你我他”活動,他們的年齡在25歲至50歲之間,按年齡分組:第1組[25,30),第2組[30,35),第3組[35,40),第4組[40,45),第5組[45,50),得到的頻率分布直方圖如圖所示. 
下表是年齡的頻數分布表:
區間 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人數 | 25 | m | p | 75 | 25 |
(1)求正整數m,p,N的值;
(2)用分層抽樣的方法,從第1、3、5組抽取6人,則第1、3、5組各抽取多少人?
(3)在(2)的條件下,從這6人中隨機抽取2人參加學校之間的宣傳交流活動,求恰有1人在第3組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)=x3+ax2+bx+c有兩個極值點x1 , x2且f(x1)=x1 , 則關于x的方程3[(f(x)]2+2af(x)+b=0的不同實根個數為( )
A.2
B.3
C.4
D.不確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程是
的參數方程是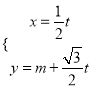 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設點![]() .
. ![]() 分別在
分別在![]() .
.![]() 上運動,若
上運動,若![]() 的最小值為1,求
的最小值為1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的奇函數,f(x+2)=f(x),當x∈(0,1]時,f(x)=1﹣2|x﹣ ![]() |,則函數g(x)=f[f(x)]﹣
|,則函數g(x)=f[f(x)]﹣ ![]() x在區間[﹣2,2]內不同的零點個數是( )
x在區間[﹣2,2]內不同的零點個數是( )
A.5
B.6
C.7
D.9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)對任意的a,b∈R,都有f(a+b)=f(a)+f(b)﹣1,且當x>0時,f(x)>1
(1)判斷并證明f(x)的單調性;
(2)若f(4)=3,解不等式f(3m2﹣m﹣2)<2.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com