設(shè)函數(shù)f (x)=ax 2+8x+3 (a<0).對(duì)于給定的負(fù)數(shù)a,有一個(gè)最大的正數(shù)l(a),使得在整個(gè) 區(qū)間[0,l(a)]上,不等式|f (x)|≤5都成立.
問(wèn):a為何值時(shí)l(a)最大?求出這個(gè)最大的l(a).證明你的結(jié)論.
【答案】
分析:利用配方法通過(guò)函數(shù)的最小值的討論,求出最大值的表達(dá)式,通過(guò)對(duì)數(shù)不等式,求出最大的正數(shù)l(a).
解答:解:f(x)=a(x+
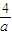
)
2+3-
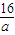
.
(1)當(dāng)3-

>5,即-8<a<0時(shí),
l(a)是方程ax
2+8x+3=5的較小根,故l(a)=
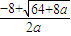
.
(2)當(dāng)3-
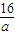
≤5,即a≤-8時(shí),
l(a)是方程ax
2+8x+3=-5的較大根,故l(a)=
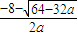
.
綜合以上,l(a)=
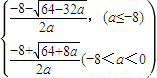
當(dāng)a≤-8時(shí),l(a)=
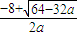
=
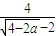
≤
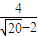
=
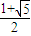
;
當(dāng)-8<a<0時(shí),l(a)=
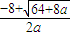
=
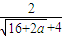
<

<
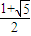
.
所以a=-8時(shí),l(a)取得最大值

.
點(diǎn)評(píng):本題考利用類(lèi)討論思想,求解二次函數(shù)的最大值,考查函數(shù)與方程的思想,分類(lèi)討論思想的應(yīng)用,難度較大.

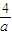 )2+3-
)2+3-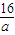 .
. >5,即-8<a<0時(shí),
>5,即-8<a<0時(shí),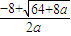 .
.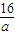 ≤5,即a≤-8時(shí),
≤5,即a≤-8時(shí),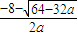 .
.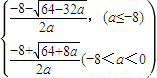
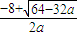 =
=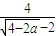 ≤
≤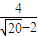 =
=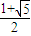 ;
;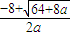 =
=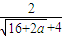 <
< <
<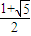 .
. .
.

