
如圖甲,在平面四邊形ABCD中,已知
 ,
, ,現將四邊形ABCD沿BD折起,使平面ABD
,現將四邊形ABCD沿BD折起,使平面ABD 平面BDC(如圖乙),設點E,F分別為棱AC,AD的中點.
平面BDC(如圖乙),設點E,F分別為棱AC,AD的中點.

(1)求證:DC 平面ABC;
平面ABC;
(2)設 ,求三棱錐A-BFE的體積.
,求三棱錐A-BFE的體積.
(1)證明:見解析;(2) .
.
【解析】
試題分析:(1)注意分析折疊前后變化的關系及不變化的關系.在圖甲中可得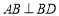 ;
;
在圖乙中,可得AB⊥CD.根據DC⊥BC,即可得到DC⊥平面ABC.
(2)首先根據E,F分別為AC,AD的中點,得到EF//CD,根據(1)知,DC⊥平面ABC,得到EF⊥平面ABC,從而得到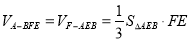
在圖甲中,根據給定角度及長度,計算“不變量”,得,BD=2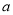 ,BC=
,BC=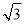
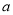 ,EF=
,EF= CD=
CD=
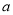 ,
,
利用體積公式計算即得所求.
解答本題的關鍵是確定“垂直關系”,這也是難點所在,平時學習中,應特別注意轉化意識的培養,等體積轉化的方法,是立體幾何中常用方法之一.
(1)證明:在圖甲中∵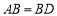 且
且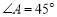 ∴
∴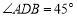 ,
,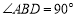
即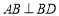 1分
1分
在圖乙中,∵平面ABD⊥平面BDC , 且平面ABD∩平面BDC=BD
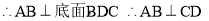 4分
4分
又 ,
,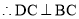 ,且
,且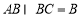 ,∴DC⊥平面ABC. 6分
,∴DC⊥平面ABC. 6分
(2)【解析】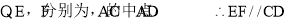 , 7分
, 7分
又由(1)知,DC⊥平面ABC,∴EF⊥平面ABC, 8分
所以,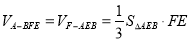 9分
9分
在圖甲中, 
由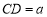 得,
得,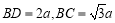 ,
,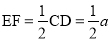 10分
10分
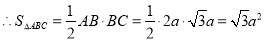 ,
,
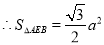 11分
11分
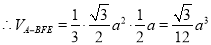 12分
12分
考點:平行關系,垂直關系,幾何體的體積.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源:2013-2014學年山東省德州市高三第二次模擬考試文科數學試卷(解析版) 題型:選擇題
已知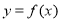 是定義在R上的偶函數,且在[0,+
是定義在R上的偶函數,且在[0,+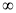 )上單調遞增,則滿足f(m)<f(1)的實數m的范圍是
)上單調遞增,則滿足f(m)<f(1)的實數m的范圍是
A. l<m<0
l<m<0
B.0<m<1
C. l<m<1
l<m<1
D. l≤m≤1
l≤m≤1
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省東營市高三4月統一質量檢測考試理科數學試卷(解析版) 題型:選擇題
偶函數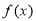 滿足
滿足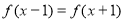 ,且在
,且在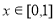 時,
時,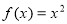 ,則關于
,則關于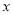 的方程
的方程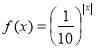 在
在 上的根的個數是
上的根的個數是
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省東營市高三4月統一質量檢測考試理科數學試卷(解析版) 題型:選擇題
“實數 ”是“復數
”是“復數 (
( 為虛數單位)的模為
為虛數單位)的模為 ”的( )
”的( )
A.充分非必要條件 B.必要非充分條件
C.充要條件 D.既非充分條件又不必要條件
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省東營市高三4月統一質量檢測考試文科數學試卷(解析版) 題型:填空題
已知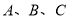 三點在球心為
三點在球心為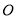 的球面上,
的球面上,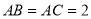 ,
,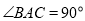 ,球心
,球心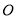 到平面
到平面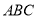 的距離為
的距離為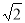 ,則球
,則球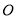 的表面積為 _ ______ .
的表面積為 _ ______ .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年山東省東營市高三4月統一質量檢測考試文科數學試卷(解析版) 題型:選擇題
已知 ,函數
,函數 在
在 上單調遞減.則
上單調遞減.則 的取值范圍是 ( )
的取值范圍是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省皖北協作區高三年級聯考理科數學試卷(解析版) 題型:選擇題
已知函數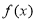 是定義在
是定義在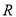 上的奇函數,對任意
上的奇函數,對任意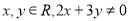 ,都有
,都有 ,若
,若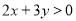 ,則( )
,則( )
A.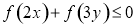
B.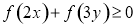
C.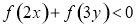
D.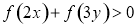
查看答案和解析>>
科目:高中數學 來源:2013-2014學年安徽省安慶市高三第二次模擬考試理科數學試卷(解析版) 題型:填空題
如果 (
( 為實常數)的展開式中所有項的系數和為0,則展開式中含
為實常數)的展開式中所有項的系數和為0,則展開式中含 項的系數為.
項的系數為.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com