
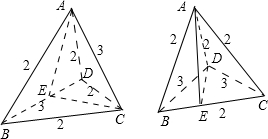
 解:根據分析可知滿足題目條件的四面體有兩種情況,也就是棱長為3的棱共面和異面
解:根據分析可知滿足題目條件的四面體有兩種情況,也就是棱長為3的棱共面和異面| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 7 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
22+(
| ||||
2×2×
|
| ||
| 12 |
1-(-
|
| ||
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 12 |
| ||
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 6 |


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com