
【題目】已知函數![]() =
=![]() .
.
(1)若不等式![]() 的解集為
的解集為![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)若對于任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)已知![]() ,若方程
,若方程![]() 在
在![]() 有解,求實數
有解,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由題意首先求得a的值,然后求解二次不等式即可得到不等式的解集;
(2)首先將原問題轉化為二次函數求最值的問題,然后結合二次函數的性質得到關于a的不等式組,求解不等式組即可求得實數a的取值范圍;
(3)首先整理所給的方程,分離參數得到關于![]() 的二次函數,結合二次函數的值域即可確定實數a的取值范圍.
的二次函數,結合二次函數的值域即可確定實數a的取值范圍.
(1)由![]() 的解集是
的解集是![]() ,可得
,可得![]() 有2個不等的實根1和2,
有2個不等的實根1和2,
由韋達定理![]() ,可得
,可得![]()
此時![]() 等價于
等價于![]() ,
,
即![]() ,解得
,解得![]() 或
或![]()
所以不等式![]() 的解集是
的解集是![]() 或
或![]() ;
;
(2)對于任意的![]() ,不等式
,不等式![]() 恒成立,
恒成立,
也即![]() 對任意的
對任意的![]() 恒成立,
恒成立,
因為![]() 二次函數開口向上,最大值在
二次函數開口向上,最大值在![]() 或
或![]() 處取得,
處取得,
所以只需滿足![]() ,解得:
,解得:![]() ,據此可得
,據此可得![]() ;
;
綜上可得,實數a的取值范圍是:![]() .
.
(3)若方程![]() 在
在![]() 有解,
有解,
可得到![]() 在
在![]() 有實數根.
有實數根.
參數分離得![]() ,則
,則![]() ,
,
結合二次函數的性質可得![]() ,
,
所以![]() ,也即
,也即![]() .
.
綜上可得,實數a的取值范圍是:![]() .
.


科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的方程為
的方程為![]() ,其焦點為
,其焦點為![]() ,
,![]() 為過焦點
為過焦點![]() 的拋物線
的拋物線![]() 的弦,過
的弦,過![]() 分別作拋物線的切線
分別作拋物線的切線![]() ,
,![]() ,設
,設![]() ,
,![]() 相交于點
相交于點![]() .
.
(1)求![]() 的值;
的值;
(2)如果圓![]() 的方程為
的方程為![]() ,且點
,且點![]() 在圓
在圓![]() 內部,設直線
內部,設直線![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分18分,第(1)小題4分,第(2)小題5分,第(3)小題9分)
設函數![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ,如果存在函數
,如果存在函數![]() ,使得函數
,使得函數![]() 的值域仍是
的值域仍是![]() ,那么稱
,那么稱![]() 是函數
是函數![]() 的一個等值域變換.
的一個等值域變換.
(1)判斷下列函數![]() 是不是函數
是不是函數![]() 的一個等值域變換?說明你的理由;
的一個等值域變換?說明你的理由;
![]() ,
,![]() ;
;
![]() ,
,![]() .
.
(2)設函數![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ,函數
,函數![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ,那么“
,那么“![]() ”是否為“
”是否為“![]() 是
是![]() 的一個等值域變換”的一個必要條件?請說明理由;
的一個等值域變換”的一個必要條件?請說明理由;
(3)設![]() 的定義域為
的定義域為![]() ,已知
,已知![]() 是
是![]() 的一個等值域變換,且函數
的一個等值域變換,且函數![]() 的定義域為
的定義域為![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面幾個命題中,假命題是( )
A. “若![]() ,則
,則![]() ”的否命題
”的否命題
B. “![]() ,函數
,函數![]() 在定義域內單調遞增”的否定
在定義域內單調遞增”的否定
C. “![]() 是函數
是函數![]() 的一個周期”或“
的一個周期”或“![]() 是函數
是函數![]() 的一個周期”
的一個周期”
D. “![]() ”是“
”是“![]() ”的必要條件
”的必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩位同學玩游戲,對于給定的實數![]() ,按下列方法操作一次產生一個新的實數:由甲、乙同時各擲一枚均勻的硬幣,如果出現兩個正面朝上或兩個反面朝上,則把
,按下列方法操作一次產生一個新的實數:由甲、乙同時各擲一枚均勻的硬幣,如果出現兩個正面朝上或兩個反面朝上,則把![]() 乘以2后再減去6;如果出現一個正面朝上,一個反面朝上,則把
乘以2后再減去6;如果出現一個正面朝上,一個反面朝上,則把![]() 除以2后再加上6,這樣就可得到一個新的實數
除以2后再加上6,這樣就可得到一個新的實數![]() ,對實數
,對實數![]() 仍按上述方法進行一次操作,又得到一個新的實數
仍按上述方法進行一次操作,又得到一個新的實數![]() ,當
,當![]() 時,甲獲勝,否則乙獲勝,若甲勝的概率為
時,甲獲勝,否則乙獲勝,若甲勝的概率為![]() ,則
,則![]() 的取值范圍是____.
的取值范圍是____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國著名數學家華羅庚先生曾說:數缺形時少直觀,形缺數時難入微,數形結合百般好,隔裂分家萬事休.在數學的學習和研究中,常用函數的圖象研究函數的性質,也常用函數的解析式來琢磨函數的圖象特征.如函數![]() 的圖象大致為( )
的圖象大致為( )
A. B.
B.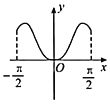
C.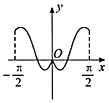 D.
D.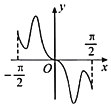
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com