
【題目】將函數f(x)=2sinx(sinx![]() cosx)﹣1圖象向右平移
cosx)﹣1圖象向右平移![]() 個單位得函數g(x)的圖象,則下列命題中正確的是( )
個單位得函數g(x)的圖象,則下列命題中正確的是( )
A.f(x)在(![]() ,
,![]() )上單調遞增
)上單調遞增
B.函數f(x)的圖象關于直線x![]() 對稱
對稱
C.g(x)=2cos2x
D.函數g(x)的圖象關于點(![]() ,0)對稱
,0)對稱
科目:高中數學 來源: 題型:
【題目】已知數集![]() ,其中
,其中![]() ,且
,且![]() ,若對
,若對![]() ,
,![]() 與
與![]() 兩數中至少有一個屬于
兩數中至少有一個屬于![]() ,則稱數集
,則稱數集![]() 具有性質
具有性質![]() .
.
(1)分別判斷數集![]() 與數集
與數集![]() 是否具有性質
是否具有性質![]() ,說明理由;
,說明理由;
(2)已知數集![]() 具有性質
具有性質![]() ,判斷數列
,判斷數列![]() ,
,![]() ,…,
,…,![]() 是否為等差數列,若是等差數列,請證明;若不是,請說明理由.
是否為等差數列,若是等差數列,請證明;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的兩焦點之間的距離為2,兩條準線間的距離為8,直線l:y=k(x-m)(m∈R)與橢圓交于P,Q兩點.
=1(a>b>0)的兩焦點之間的距離為2,兩條準線間的距離為8,直線l:y=k(x-m)(m∈R)與橢圓交于P,Q兩點.
(1) 求橢圓C的方程;
(2) 設橢圓的左頂點為A,記直線AP,AQ的斜率分別為k1,k2.①若m=0,求k1k2的值;②若k1k2=-![]() ,求實數m的值.
,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級共有50名同學(男女各占一半),為弘揚傳統文化,班委組織了“古詩詞男女對抗賽”,將同學隨機分成25組,每組男女同學各一名,每名同學均回答同樣的五個不同問題,答對一題得一分,答錯或不答得零分,總分5分為滿分.最后25組同學得分如下表:
組別號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
男同學得分 | 5 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 4 | 4 | 5 | 5 | 4 |
女同學得分 | 4 | 3 | 4 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 3 | 5 |
分差 | 1 | 1 | 1 | 0 | -1 | 0 | 1 | -1 | -1 | -1 | 0 | 2 | -1 |
組別號 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
男同學得分 | 4 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 4 | 3 | 3 | |
女同學得分 | 5 | 3 | 4 | 5 | 4 | 3 | 5 | 5 | 3 | 4 | 5 | 5 | |
分差 | -1 | 0 | 0 | -1 | 0 | 1 | 0 | 0 | 2 | 0 | -2 | -2 | |
(I)完成![]() 列聯表,并判斷是否有90%的把握認為“該次對抗賽是否得滿分”與“同學性別”有關;
列聯表,并判斷是否有90%的把握認為“該次對抗賽是否得滿分”與“同學性別”有關;
(Ⅱ)某課題研究小組假設各組男女同學分差服從正態分布![]() ,首先根據前20組男女同學的分差確定
,首先根據前20組男女同學的分差確定![]() 和
和![]() ,然后根據后面5組同學的分差來檢驗模型,檢驗方法是:記后面5組男女同學分差與
,然后根據后面5組同學的分差來檢驗模型,檢驗方法是:記后面5組男女同學分差與![]() 的差的絕對值分別為
的差的絕對值分別為![]() ,若出現下列兩種情況之一,則不接受該模型,否則接受該模型.①存在
,若出現下列兩種情況之一,則不接受該模型,否則接受該模型.①存在![]() ;②記滿足
;②記滿足![]() 的i的個數為k,在服從正態分布
的i的個數為k,在服從正態分布![]() 的總體(個體數無窮大)中任意取5個個體,其中落在區間
的總體(個體數無窮大)中任意取5個個體,其中落在區間![]() 內的個體數大于或等于k的概率為P,
內的個體數大于或等于k的概率為P,![]() .
.
試問該課題研究小組是否會接受該模型.
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
參考公式和數據: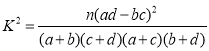
![]() ,
,![]() ;若
;若![]() ,有
,有![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+ax+blnx(a,b∈R),曲線y=f(x)在點(1,f(1))處的切線方程為2x﹣y﹣2=0.
(1)判斷f(x)在定義域內的單調性,并說明理由;
(2)若對任意的x∈(1,+∞),不等式f(x)≤m(ex﹣1﹣1)恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國制造2025》是經國務院總理李克強簽批,由國務院于2015年5月印發的部署全面推進實施制造強國的戰略文件,是中國實施制造強國戰略第一個十年的行動綱領.制造業是國民經濟的主體,是立國之本、興國之器、強國之基.發展制造業的基本方針為質量為先,堅持把質量作為建設制造強國的生命線.某制造企業根據長期檢測結果,發現生產的產品質量與生產標準的質量差都服從正態分布N(μ,σ2),并把質量差在(μ﹣σ,μ+σ)內的產品為優等品,質量差在(μ+σ,μ+2σ)內的產品為一等品,其余范圍內的產品作為廢品處理.優等品與一等品統稱為正品.現分別從該企業生產的正品中隨機抽取1000件,測得產品質量差的樣本數據統計如下:
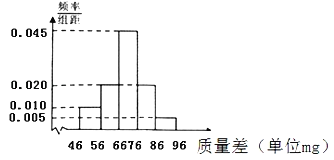
(1)根據頻率分布直方圖,求樣本平均數![]()
(2)根據大量的產品檢測數據,檢查樣本數據的方差的近似值為100,用樣本平均數![]() 作為μ的近似值,用樣本標準差s作為σ的估計值,求該廠生產的產品為正品的概率.(同一組中的數據用該組區間的中點值代表)
作為μ的近似值,用樣本標準差s作為σ的估計值,求該廠生產的產品為正品的概率.(同一組中的數據用該組區間的中點值代表)
[參考數據:若隨機變量ξ服從正態分布N(μ,σ2),則:P(μ﹣σ<ξ≤μ+σ)≈0.6827,P(μ﹣2σ<ξ≤μ+2σ)≈0.9545,P(μ﹣3σ<ξ≤μ+3σ)≈0.9973.
(3)假如企業包裝時要求把3件優等品球和5件一等品裝在同一個箱子中,質檢員每次從箱子中摸出三件產品進行檢驗,記摸出三件產品中優等品球的件數為X,求X的分布列以及期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,
,![]()
(1)求證:數列![]() 是等比數列;
是等比數列;
(2)若![]() ,是否存在q的某些取值,使數列
,是否存在q的某些取值,使數列![]() 中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使數列
,使數列![]() 中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】很多關于整數規律的猜想都通俗易懂,吸引了大量的數學家和數學愛好者,有些猜想已經被數學家證明,如“費馬大定理”,但大多猜想還未被證明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的內容是:對于每一個正整數,如果它是奇數,則將它乘以![]() 再加1;如果它是偶數,則將它除以
再加1;如果它是偶數,則將它除以![]() ;如此循環,最終都能夠得到
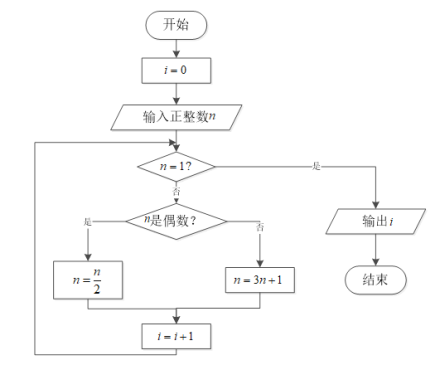
;如此循環,最終都能夠得到![]() .下圖為研究“角谷猜想”的一個程序框圖.若輸入
.下圖為研究“角谷猜想”的一個程序框圖.若輸入![]() 的值為
的值為![]() ,則輸出i的值為( )
,則輸出i的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,過原點
,過原點![]() 的直線(與坐標軸不重合)與橢圓
的直線(與坐標軸不重合)與橢圓![]() 交于點
交于點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 分別與
分別與![]() 軸交于點
軸交于點![]() 、
、![]() .
.
(1)若![]() ,求點
,求點![]() 的橫坐標;
的橫坐標;
(2)設直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com