
【題目】給定橢圓![]() ,稱圓心在坐標原點
,稱圓心在坐標原點![]() ,半徑為
,半徑為![]() 的圓是橢圓
的圓是橢圓![]() 的“伴橢圓”,若橢圓
的“伴橢圓”,若橢圓![]() 右焦點坐標為
右焦點坐標為![]() ,且過點
,且過點![]() .
.
(1)求橢圓![]() 的“伴橢圓”方程;
的“伴橢圓”方程;
(2)在橢圓![]() 的“伴橢圓”上取一點
的“伴橢圓”上取一點![]() ,過該點作橢圓的兩條切線
,過該點作橢圓的兩條切線![]() 、
、![]() ,證明:兩線垂直;
,證明:兩線垂直;
(3)在雙曲線![]() 上找一點
上找一點![]() 作橢圓
作橢圓![]() 的兩條切線,分別交于切點
的兩條切線,分別交于切點![]() 、
、![]() 使得
使得![]() ,求滿足條件的所有點
,求滿足條件的所有點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1) 利用![]() 和
和![]() 聯(lián)立解方程可得;
聯(lián)立解方程可得;
(2) 設(shè)切線方程為:![]() ,代入橢圓
,代入橢圓![]() 的方程,利用判別式等于0,可得關(guān)于斜率
的方程,利用判別式等于0,可得關(guān)于斜率![]() 的一元二次方程,利用韋達定理可得斜率之積為
的一元二次方程,利用韋達定理可得斜率之積為![]() ,從而可證兩條切線垂直;
,從而可證兩條切線垂直;
(3) 設(shè)經(jīng)過點![]() 與橢圓相切的直線為:
與橢圓相切的直線為:![]() ,代入橢圓
,代入橢圓![]() 的方程,利用判別式為0, 可得關(guān)于斜率
的方程,利用判別式為0, 可得關(guān)于斜率![]() 的一元二次方程,然后根據(jù)斜率之積為
的一元二次方程,然后根據(jù)斜率之積為![]() 可得點
可得點![]() 的軌跡方程為
的軌跡方程為![]() ,最后聯(lián)立此方程與雙曲線方程可解得
,最后聯(lián)立此方程與雙曲線方程可解得![]() 的坐標即可.
的坐標即可.
(1)依題意可得,![]() ,所以
,所以![]() ,①
,①
又橢圓![]() 過點
過點![]() ,所以
,所以![]() ②
②
由①②可得![]() ,
,
橢圓![]() 的“伴橢圓”方程為:
的“伴橢圓”方程為:![]() .
.
(2)由(1)可得橢圓![]() ,
,
設(shè)切線方程為:![]() ,將其代入橢圓
,將其代入橢圓![]() ,消去
,消去![]() 并整理得:
并整理得:
![]() ,
,
由![]() ,
,
得![]() ,
,
設(shè)![]() ,
,![]() 的斜率為
的斜率為![]() ,則
,則![]() ,
,
所以兩條切線垂直.
(3)當兩條切線![]() 的斜率存在時,設(shè)經(jīng)過點
的斜率存在時,設(shè)經(jīng)過點![]() 與橢圓相切的直線為:
與橢圓相切的直線為:![]() ,
,
則
消去![]() 并整理得,
并整理得,![]() ,
,
所以![]() ,
,
經(jīng)過化簡得到:![]() ,
,
設(shè)兩條切線![]() 的斜率分別為
的斜率分別為![]() ,
,
則![]() ,
,
因為![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
當兩條切線![]() 的斜率不存在時,
的斜率不存在時,![]() 也滿足
也滿足![]() ,
,
所以![]() 的軌跡為橢圓的”伴隨圓”,其方程為:
的軌跡為橢圓的”伴隨圓”,其方程為:![]() ,
,
聯(lián)立 ,解得
,解得 ,
,
所以 或
或 或
或 或
或 ,
,
所以滿足條件的所有點![]() 的坐標為:
的坐標為: ![]() 或
或![]() 或
或![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
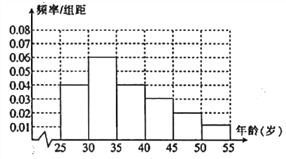
【題目】某高校進行社會實踐,對![]() 歲的人群隨機抽取 1000 人進行了一次是否開通“微博”的調(diào)查,開通“微博”的為“時尚族”,否則稱為“非時尚族”.通過調(diào)查得到到各年齡段人數(shù)的頻率分布直方圖如圖所示,其中在
歲的人群隨機抽取 1000 人進行了一次是否開通“微博”的調(diào)查,開通“微博”的為“時尚族”,否則稱為“非時尚族”.通過調(diào)查得到到各年齡段人數(shù)的頻率分布直方圖如圖所示,其中在![]() 歲,
歲, ![]() 歲年齡段人數(shù)中,“時尚族”人數(shù)分別占本組人數(shù)的
歲年齡段人數(shù)中,“時尚族”人數(shù)分別占本組人數(shù)的![]() 、
、![]() .
.
(1)求![]() 歲與
歲與![]() 歲年齡段“時尚族”的人數(shù);
歲年齡段“時尚族”的人數(shù);
(2)從![]() 歲和
歲和![]() 歲年齡段的“時尚族”中,采用分層抽樣法抽取6人參加網(wǎng)絡(luò)時尚達人大賽,其中兩人作為領(lǐng)隊.求領(lǐng)隊的兩人年齡都在
歲年齡段的“時尚族”中,采用分層抽樣法抽取6人參加網(wǎng)絡(luò)時尚達人大賽,其中兩人作為領(lǐng)隊.求領(lǐng)隊的兩人年齡都在![]() 歲內(nèi)的概率。
歲內(nèi)的概率。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某班共有![]() 名學生,已知以下信息:
名學生,已知以下信息:
①男生共有![]() 人;
人;
②女團員共有![]() 人;
人;
③住校的女生共有![]() 人;
人;
④不住校的團員共有![]() 人;
人;
⑤住校的男團員共有![]() 人;
人;
⑥男生中非團員且不住校的共有![]() 人;
人;
⑦女生中非團員且不住校的共有![]() 人.
人.
根據(jù)以上信息,該班住校生共有______人![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為更好地落實農(nóng)民工工資保證金制度,南方某市勞動保障部門調(diào)查了![]() 年下半年該市
年下半年該市![]() 名農(nóng)民工(其中技術(shù)工、非技術(shù)工各
名農(nóng)民工(其中技術(shù)工、非技術(shù)工各![]() 名)的月工資,得到這
名)的月工資,得到這![]() 名農(nóng)民工月工資的中位數(shù)為
名農(nóng)民工月工資的中位數(shù)為![]() 百元(假設(shè)這
百元(假設(shè)這![]() 名農(nóng)民工的月工資均在
名農(nóng)民工的月工資均在![]() (百元)內(nèi))且月工資收入在
(百元)內(nèi))且月工資收入在![]() (百元)內(nèi)的人數(shù)為
(百元)內(nèi)的人數(shù)為![]() ,并根據(jù)調(diào)查結(jié)果畫出如圖所示的頻率分布直方圖:
,并根據(jù)調(diào)查結(jié)果畫出如圖所示的頻率分布直方圖:

(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知這![]() 名農(nóng)民工中月工資高于平均數(shù)的技術(shù)工有
名農(nóng)民工中月工資高于平均數(shù)的技術(shù)工有![]() 名,非技術(shù)工有
名,非技術(shù)工有![]() 名,則能否在犯錯誤的概率不超過
名,則能否在犯錯誤的概率不超過![]() 的前提下認為是不是技術(shù)工與月工資是否高于平均數(shù)有關(guān)系?
的前提下認為是不是技術(shù)工與月工資是否高于平均數(shù)有關(guān)系?
參考公式及數(shù)據(jù): ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓![]() 經(jīng)過
經(jīng)過![]() 兩點,且圓心
兩點,且圓心![]() 在直線
在直線![]() 上.
上.

(1)求圓![]() 的方程;
的方程;
(2)已知過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交截得的弦長為
相交截得的弦長為![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)已知點![]() ,在平面內(nèi)是否存在異于點
,在平面內(nèi)是否存在異于點![]() 的定點
的定點![]() ,對于圓
,對于圓![]() 上的任意動點
上的任意動點![]() ,都有
,都有![]() 為定值?若存在求出定點
為定值?若存在求出定點![]() 的坐標,若不存在說明理由.
的坐標,若不存在說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義:若數(shù)列![]() 中存在
中存在![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 及
及![]() 均為正整數(shù),且
均為正整數(shù),且![]() (
(![]() ),則稱數(shù)列
),則稱數(shù)列![]() 為“
為“![]() 數(shù)列”.
數(shù)列”.
(1)若數(shù)列![]() 的前
的前![]() 項和
項和![]() ,求證:
,求證:![]() 是“
是“![]() 數(shù)列”;
數(shù)列”;
(2)若![]() 是首項為1,公比為
是首項為1,公比為![]() 的等比數(shù)列,判斷
的等比數(shù)列,判斷![]() 是否是“
是否是“![]() 數(shù)列”,說明理由;
數(shù)列”,說明理由;
(3)若![]() 是公差為
是公差為![]() (
(![]() )的等差數(shù)列且
)的等差數(shù)列且![]() (
(![]() ),
),![]() ,求證:數(shù)列
,求證:數(shù)列![]() 是“
是“![]() 數(shù)列”.
數(shù)列”.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com