
【題目】如圖,圓F:![]() 和拋物線
和拋物線![]() ,過F的直線與拋物線和圓依次交于A、B、C、D四點,求
,過F的直線與拋物線和圓依次交于A、B、C、D四點,求![]() 的值是( )
的值是( )

A.1B.2C.3D.無法確定
【答案】A
【解析】
可分兩類討論,若直線的斜率不存在,則直線方程為x=1,代入拋物線方程和圓的方程,可直接得到ABCD四個點的坐標,從而|AB||CD|=1.若直線的斜率存在,設為直線方程為y=k(x-1),不妨設A(x1,y1),D(x2,y2),過A、D分別作拋物線準線的垂線,由拋物線的定義,|AF|=x1+1,|DF|=x2+1,把直線方程與拋物線方程聯立,消去y可得k2x2-(2k2+4)x+k2=0,利用韋達定理及|AB|=|AF|-|BF|=x1,|CD|=|DF|-|CF|=x2,可求|AB||CD|的值.
解:若直線的斜率不存在,則直線方程為x=1,代入拋物線方程和圓的方程,可直接得到ABCD四個點的坐標為(1,2)(1,1)(1,-1)(1,-2),所以|AB|=1,|CD|=1,從而|AB||CD|=1.若直線的斜率存在,設為k,因為直線過拋物線的焦點(1,0),則直線方程為y=k(x-1),不妨設A(x1,y1),D(x2,y2),過A、D分別作拋物線準線的垂線,由拋物線的定義,|AF|=x1+1,|DF|=x2+1,把直線方程與拋物線方程聯立,消去y可得k2x2-(2k2+4)x+k2=0,由韋達定理有 x1x2=1而拋物線的焦點F同時是已知圓的圓心,所以|BF|=|CF|=R=1
從而有|AB|=|AF|-|BF|=x1,|CD|=|DF|-|CF|=x2.
所以|AB||CD|=x1x2=1
故選:A.


科目:高中數學 來源: 題型:
【題目】在一次田徑比賽中,35名運動員的成績(單位:分鐘)的莖葉圖如圖所示。

若將運動員按成績由好到差編為1—35號,再用系統抽樣方法從中抽取5人,則其中成績在區間![]() 上的運動員人數為
上的運動員人數為
A.6B.5C.4D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定橢圓![]() ,稱圓心在坐標原點
,稱圓心在坐標原點![]() ,半徑為
,半徑為![]() 的圓是橢圓
的圓是橢圓![]() 的“伴橢圓”,若橢圓
的“伴橢圓”,若橢圓![]() 右焦點坐標為
右焦點坐標為![]() ,且過點
,且過點![]() .
.
(1)求橢圓![]() 的“伴橢圓”方程;
的“伴橢圓”方程;
(2)在橢圓![]() 的“伴橢圓”上取一點
的“伴橢圓”上取一點![]() ,過該點作橢圓的兩條切線
,過該點作橢圓的兩條切線![]() 、
、![]() ,證明:兩線垂直;
,證明:兩線垂直;
(3)在雙曲線![]() 上找一點
上找一點![]() 作橢圓
作橢圓![]() 的兩條切線,分別交于切點
的兩條切線,分別交于切點![]() 、
、![]() 使得
使得![]() ,求滿足條件的所有點
,求滿足條件的所有點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列各項均非零,且存在常數![]() ,對任意
,對任意![]() ,
,![]() 恒成立,則成這樣的數列為“類等比數列”,例如等比數列一定為類等比數列,則:
恒成立,則成這樣的數列為“類等比數列”,例如等比數列一定為類等比數列,則:
(1)各項均非零的等差數列是否可能為“類等比數列”?若可能,請舉例;若不能,說明理由;
(2)已知數列![]() 為“類等比數列”,且
為“類等比數列”,且![]() ,是否存在常數
,是否存在常數![]() ,使得
,使得![]() 恒成立?
恒成立?
(3)已知數列![]() 為“類等比數列”,且
為“類等比數列”,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
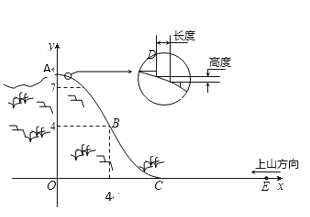
【題目】某旅游勝地欲開發一座景觀山,從山的側面進行勘測,迎面山坡線![]() 由同一平面的兩段拋物線組成,其中
由同一平面的兩段拋物線組成,其中![]() 所在的拋物線以
所在的拋物線以![]() 為頂點、開口向下,
為頂點、開口向下,![]() 所在的拋物線以
所在的拋物線以![]() 為頂點、開口向上,以過山腳(點
為頂點、開口向上,以過山腳(點![]() )的水平線為
)的水平線為![]() 軸,過山頂(點
軸,過山頂(點![]() )的鉛垂線為
)的鉛垂線為![]() 軸建立平面直角坐標系如圖(單位:百米).已知
軸建立平面直角坐標系如圖(單位:百米).已知![]() 所在拋物線的解析式
所在拋物線的解析式![]() ,
,![]() 所在拋物線的解析式為
所在拋物線的解析式為![]()
(1)求![]() 值,并寫出山坡線
值,并寫出山坡線![]() 的函數解析式;
的函數解析式;
(2)在山坡上的700米高度(點![]() )處恰好有一小塊平地,可以用來建造索道站,索道的起點選擇在山腳水平線上的點
)處恰好有一小塊平地,可以用來建造索道站,索道的起點選擇在山腳水平線上的點![]() 處,
處,![]() (米),假設索道
(米),假設索道![]() 可近似地看成一段以
可近似地看成一段以![]() 為頂點、開口向上的拋物線
為頂點、開口向上的拋物線![]() 當索道在
當索道在![]() 上方時,索道的懸空高度有最大值,試求索道的最大懸空高度;
上方時,索道的懸空高度有最大值,試求索道的最大懸空高度;
(3)為了便于旅游觀景,擬從山頂開始、沿迎面山坡往山下鋪設觀景臺階,臺階每級的高度為20厘米,長度因坡度的大小而定,但不得少于20厘米,每級臺階的兩端點在坡面上(見圖).試求出前三級臺階的長度(精確到厘米),并判斷這種臺階能否一直鋪到山腳,簡述理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
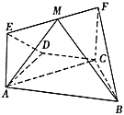
【題目】如圖,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,![]() .
.
(1)求證:![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上運動,設平面
上運動,設平面![]() 與平面
與平面![]() 所成二面角的平面角為
所成二面角的平面角為![]() (
(![]() ),試求
),試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合![]() 是實數集
是實數集![]() 的子集,如果正實數
的子集,如果正實數![]() 滿足:對任意
滿足:對任意![]() 都存在
都存在![]() 使得
使得![]() 則稱
則稱![]() 為集合
為集合![]() 的一個“跨度”,已知三個命題:
的一個“跨度”,已知三個命題:
(1)若![]() 為集合
為集合![]() 的“跨度”,則
的“跨度”,則![]() 也是集合
也是集合![]() 的“跨度”;
的“跨度”;
(2)集合![]() 的“跨度”的最大值是4;
的“跨度”的最大值是4;
(3)![]() 是集合
是集合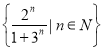 的“跨度”.
的“跨度”.
這三個命題中正確的個數是()
A.0B.1C.2D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com