
已知函數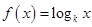 (
(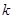 為常數,
為常數,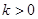 且
且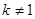 ),且數列
),且數列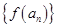 是首項為4,公差為2的等差數列。
是首項為4,公差為2的等差數列。
(Ⅰ)求證:數列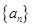 是等比數列;
是等比數列;
(Ⅱ)若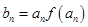 ,當
,當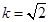 時,求數列
時,求數列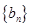 的前n項和
的前n項和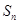 。
。
(Ⅰ)詳見解析;(Ⅱ) .
.
【解析】
試題分析:(Ⅰ)數列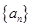 是等比數列,只需證明
是等比數列,只需證明 等于一個與
等于一個與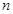 無關的常數即可,由已知數列
無關的常數即可,由已知數列 是首項為4,公差為2的等差數列,故
是首項為4,公差為2的等差數列,故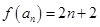 ,即
,即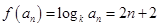 ,可求得
,可求得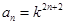 ,代入
,代入 即可數列
即可數列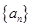 是等比數列;(Ⅱ)若
是等比數列;(Ⅱ)若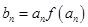 ,當
,當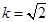 時,求數列
時,求數列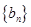 的前
的前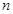 項和
項和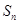 ,首先求出數列
,首先求出數列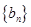 的通項公式,由(Ⅰ)可知
的通項公式,由(Ⅰ)可知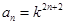 ,故
,故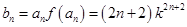 ,這是一個等差數列與一個等比數列對應項積所組成的數列,可利用錯位相減法來求和,可求得
,這是一個等差數列與一個等比數列對應項積所組成的數列,可利用錯位相減法來求和,可求得 .
.
試題解析:(Ⅰ)由題意知f(an)=4+(n-1)×2=2n+2, (2分)
即logkan=2n+2,∴an=k2n+2, (3分)
∴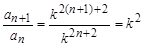 .
(5分)
.
(5分)
∵常數k>0且k≠1,∴k2為非零常數,
∴數列{an}是以k4為首項,k2為公比的等比數列。 (6分)
(Ⅱ)由(1)知,bn=anf(an)=k2n+2·(2n+2),
當k=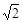 時,bn=(2n+2)·2n+1=(n+1)·2n+2.
(8分)
時,bn=(2n+2)·2n+1=(n+1)·2n+2.
(8分)
∴Sn=2·23+3·24+4·25++(n+1)·2n+2, ①
2Sn=2·24+3·25++n·2n+2+(n+1)·2n+3, ② (10分)
②-①,得Sn=―2·23―24―25――2n+2+(n+1)·2n+3
=―23―(23+24+25++2n+2)+(n+1)·2n+3,
∴Sn=―23― +(n+1)·2n+3=n·2n+3.
(12分)
+(n+1)·2n+3=n·2n+3.
(12分)
考點:等差數列與等比數列的綜合,數列求和.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:
已知函數![]() (
(![]() 為常數,且
為常數,且![]() )的圖象過點
)的圖象過點![]() ,且函數
,且函數![]() 的最大值為2。
的最大值為2。
(1)、求函數![]() 的解析式,并寫出其單調遞增區間。
的解析式,并寫出其單調遞增區間。
(2)、若函數![]() 的圖象按向量
的圖象按向量![]() 作移動距離最小的平移后,使所的圖象關于y軸對稱,求出向量
作移動距離最小的平移后,使所的圖象關于y軸對稱,求出向量![]() 的坐標及平移后的圖象對應的函數解析式。
的坐標及平移后的圖象對應的函數解析式。
查看答案和解析>>
科目:高中數學 來源: 題型:
已知函數![]() 、
、![]() 為 常數,且
為 常數,且![]() )的圖象過 點(0,
)的圖象過 點(0,![]() ),且函數
),且函數![]() 的最大值為2。
的最大值為2。
⑴求函數![]() 的解析式,并寫出其單調遞增區間;
的解析式,并寫出其單調遞增區間;
⑵若函數![]() 的圖象按向量
的圖象按向量![]() 作移動距離最小的平移后,使所得圖象關于
作移動距離最小的平移后,使所得圖象關于![]() 軸對稱,求出向量
軸對稱,求出向量![]() 的坐標及平移后的圖象對應的函數解析式.
的坐標及平移后的圖象對應的函數解析式.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省高三第二次階段性考試數學試卷(解析版) 題型:選擇題
已知函數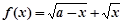 (
(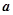 為常數,且
為常數,且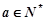 ),對于定義域內的任意兩個實數
),對于定義域內的任意兩個實數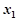 、
、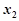 ,恒有
,恒有 成立,則正整數
成立,則正整數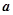 可以取的值有
可以取的值有
A.4個 B.5個 C.6 個 D.7個
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省高三10月階段性測試理科數學試卷(解析版) 題型:選擇題
已知函數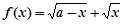 (
(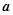 為常數,且
為常數,且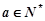 ),對于定義域內的任意兩個實數
),對于定義域內的任意兩個實數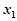 、
、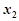 ,恒有
,恒有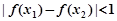 成立,則正整數
成立,則正整數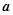 可以取的值有
可以取的值有
A.4個 B.5個 C.6 個 D.7個
查看答案和解析>>
科目:高中數學 來源:2010年廣東省高考沖刺強化訓練試卷二文科數學 題型:解答題
(本小題滿分14分)
已知函數 (
(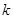 為常數,
為常數, 且
且 ),且數列
),且數列 是首項為4,
是首項為4,
公差為2的等差數列.
(Ⅰ)求證:數列 是等比數列;
是等比數列;
(Ⅱ) 若 ,當
,當 時,求數列
時,求數列 的前
的前 項和
項和 ;
;
(III)若 ,且
,且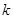 >1,比較
>1,比較 與
與 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com