
(本小題滿分14分)已知函數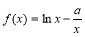 .
.
(1)若a>0,試判斷 在定義域內的單調性;
在定義域內的單調性;
(2)若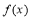 在
在 上的最小值為
上的最小值為 ,求a的值;
,求a的值;
(3)若 在
在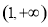 上恒成立,求a的取值范圍
上恒成立,求a的取值范圍
(1)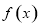 在
在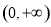 上是單調遞增函數;(2)
上是單調遞增函數;(2)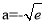 ;(3)
;(3)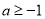 .
.
【解析】
試題分析:(1)由題意知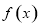 的定義域為
的定義域為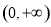 ,求導數知
,求導數知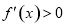 ,
, 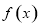 在
在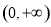 上是單調遞增函數;
上是單調遞增函數;
(2)討論①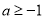 ;②
;②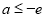 ;③
;③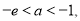 等幾種情況,通過研究函數的單調性、確定最小值,建立方程求解.
等幾種情況,通過研究函數的單調性、確定最小值,建立方程求解.
(3)由已知得到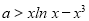 ,
,
令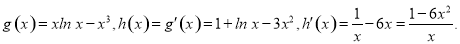 .
.
通過討論函數的單調性明確 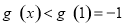 得解.
得解.
試題解析:(1)由題意知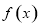 的定義域為
的定義域為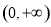 ,且
,且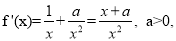 ,
,
∴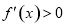 , 故
, 故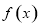 在
在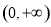 上是單調遞增函數 4分
上是單調遞增函數 4分
(2)由(1)可知, 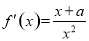 .
.
①若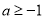 ,則
,則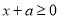 ,即
,即 在
在 上恒成立, 此時
上恒成立, 此時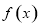 在
在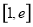 上為增函數,
上為增函數,
∴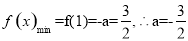 (舍去) 6分
(舍去) 6分
②若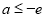 ,則
,則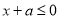 ,即
,即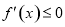 在
在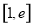 上恒成立, 此時
上恒成立, 此時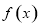 在
在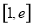 上為減函數,
上為減函數,
∴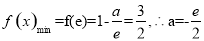 (舍去) 8分
(舍去) 8分
③若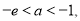 令
令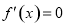 得
得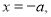
當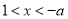 時,
時, 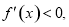 ∴
∴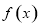 在
在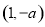 上為減函數;
上為減函數;
當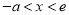 時,
時, 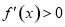 ,∴
,∴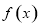 在
在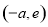 上為增函數,
上為增函數,
∴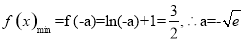 .綜上所述,
.綜上所述, 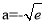 10分
10分
(3)∵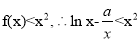 .又
.又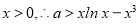 ,
,
令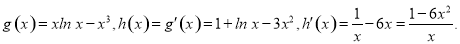 .
.
∵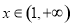 時,
時, 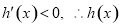 在
在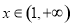 上是減函數.
上是減函數.
∴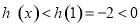 ,即
,即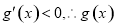 在
在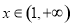 上也是減函數.
上也是減函數.
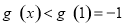 ,∴當
,∴當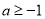 時,
時, 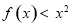 在
在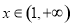 上恒成立 14分
上恒成立 14分
考點:1.應用導數研究函數的單調性、極值、最值;2.轉化與化歸思想.


科目:高中數學 來源:2015屆山東省菏澤市高三上學期期中聯考理科數學試卷(解析版) 題型:填空題
已知角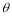 的頂點與原點重合,始邊與x軸的正半軸重合,終邊在直線y=2x上,
的頂點與原點重合,始邊與x軸的正半軸重合,終邊在直線y=2x上,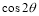 =__________.
=__________.
查看答案和解析>>
科目:高中數學 來源:2015屆山東省菏澤市高三上學期期中聯考文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)設命題p:實數x滿足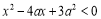 ,其中
,其中 ;命題q:實數
;命題q:實數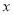 滿足
滿足 且
且 的必要不充分條件,求實數
的必要不充分條件,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com