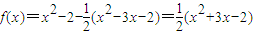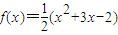已知函數f(t)滿足對任意實數x,y都有f(x+y)=f(x)+f(y)+xy+1,且f(-2)=-2.
(1)求f(1)的值;
(2)證明:對一切大于1的正整數t,恒有f(t)>t;
(3)試求滿足f(t)=t的整數t的個數,并說明理由.
【答案】
分析:(1)對抽象函數所滿足的關系式,進行賦值,分別令x=y=0,x=y=-1,x=1,y=-1即可求f(1);
(2)對抽象函數所滿足的關系式,令x=n,y=1,代入化簡即可證明;
(3)對抽象函數所滿足的關系式,令y=-x,討論x為整數的情況,轉化為二次函數與方程問題解決即可.
解答:解:(1)x=y=0得f(0)=-1
x=y=-1得f(-2)=2f(-1)+2
而f(-2)=-2,∴f(-1)=-2
x=1,y=-1得f(0)=f(1)+f(-1)
∴f(1)=1.
(2)x=n,y=1得f(n+1)=f(n)+f(1)+n+1=f(n)+n+2
∴f(n+1)-f(n)=n+2,
∴當n∈N
+時,f(n)=f(1)+[3+4++(n+1)]=
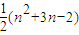
則f(n)-n=
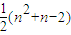
而當n∈N
+,且n>1時,n
2+n-2>0,
∴f(n)>n,則對一切大于1的正整數t,恒有f(t)>t.
(3)∵y=-x時f(x-x)=f(x)+f(-x)+1-x
2∴f(x)=x
2-2-f(-x)
∵當x∈N
+時由(2)知

當x=0時,f(0)=-1=

當x為負整數時,-x∈N
+,則
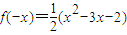
,
∴
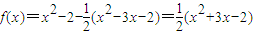
故對一切x∈Z時,有
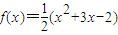
∴當t∈Z時,由f(t)=t得t
2+t-2=0,即t=1或t=2
∴滿足f(t)=t的整數t有兩個.
點評:本題考查抽象函數的求值、計算與證明問題,抽象函數是相對于函數有具體解析式而言的,賦值法是解決抽象函數的一把“利劍”,本題屬于中檔題.

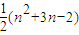 則f(n)-n=
則f(n)-n=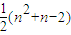


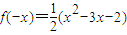 ,
,