
【題目】在平面直角坐標系![]() 中,①已知點
中,①已知點![]() ,直線
,直線![]() :
:![]() ,動點
,動點![]() 滿足到點
滿足到點![]() 的距離與到直線
的距離與到直線![]() 的距離之比為
的距離之比為![]() ;②已知圓
;②已知圓![]() 的方程為
的方程為![]() ,直線
,直線![]() 為圓
為圓![]() 的切線,記點
的切線,記點![]() 到直線
到直線![]() 的距離分別為
的距離分別為![]() ,動點
,動點![]() 滿足
滿足![]() ;③點
;③點![]() ,
,![]() 分別在
分別在![]() 軸,
軸,![]() 軸上運動,且
軸上運動,且![]() ,動點
,動點![]() 滿足
滿足![]() .
.
(1)在①,②,③這三個條件中任選一個,求動點![]() 的軌跡方程;
的軌跡方程;
(2)記(1)中的軌跡為![]() ,經過點
,經過點![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,若線段
兩點,若線段![]() 的垂直平分線與
的垂直平分線與![]() 軸相交于點
軸相交于點![]() ,求點
,求點![]() 縱坐標的取值范圍.
縱坐標的取值范圍.
【答案】(1)不論選哪種條件,動點![]() 的軌跡方程
的軌跡方程![]() (2)
(2)![]()
【解析】
(1)選①,可以用直接法求軌跡方程,選②,可以用待定系數法求軌跡方程,選③,可以用代入法求軌跡方程;(2)設![]() ,當
,當![]() 斜率不存在時,
斜率不存在時,![]() ,當
,當![]() 斜率不存在時,求出
斜率不存在時,求出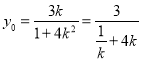 ,得到
,得到![]() 或
或![]() ,綜合即得解.
,綜合即得解.
(1)若選①,
設![]() ,根據題意,
,根據題意,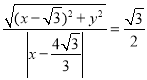 ,
,
整理得![]() ,
,
所以所求的軌跡方程為![]() .
.
若選②,
設![]() ,直線
,直線![]() 與圓相切于點
與圓相切于點![]() ,
,
則![]() ,
,
由橢圓定義知,點![]() 的軌跡是以
的軌跡是以![]() 為焦點的橢圓,
為焦點的橢圓,
所以![]() ,
,
故![]() ,
,
所以所求的軌跡方程為![]() .
.
若選③,
設![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,
因為![]() ,
,
所以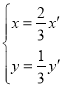 ,
,
整理得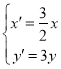 ,
,
代入![]() 得
得![]() ,
,
所以所求的軌跡方程為![]()
(2)設![]() ,當
,當![]() 斜率不存在時,
斜率不存在時,![]() ,
,
當![]() 斜率存在時,
斜率存在時,
設直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]() ,
,
由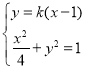 ,消去
,消去![]() 并整理,
并整理,
得![]() ,
,
![]() 恒成立,
恒成立,![]() ,
,
設線段![]() 的中點為
的中點為![]() ,
,
則![]() ,
,
所以線段![]() 的垂直平分線方程為:
的垂直平分線方程為:
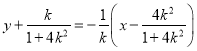 ,
,
令![]() ,得
,得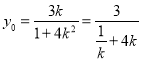 ,
,
當![]() 時,
時,![]() ,
,
當且僅當![]() 時,取等號,所以
時,取等號,所以![]() ;
;
當![]() 時,
時,![]() ,
,
當且僅當![]() 時,取等號,所以
時,取等號,所以![]() ;
;
綜上,點![]() 縱坐標的取值范圍是
縱坐標的取值范圍是![]()


科目:高中數學 來源: 題型:
【題目】CES是世界上最大的消費電子技術展,也是全球最大的消費技術產業盛會.2020CES消費電子展于2020年1月7日—10日在美國拉斯維加斯舉辦.在這次CES消費電子展上,我國某企業發布了全球首款彩色水墨屏閱讀手機,驚艷了全場.若該公司從7名員工中選出3名員工負責接待工作(這3名員工的工作視為相同的工作),再選出2名員工分別在上午、下午講解該款手機性能,若其中甲和乙至多有1人負責接待工作,則不同的安排方案共有__________種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() ,交
,交![]() 于點
于點![]() .將
.將![]() 沿線段
沿線段![]() 折起,使得點
折起,使得點![]() 在平面
在平面![]() 內的投影恰好是點
內的投影恰好是點![]() ,如圖.
,如圖.
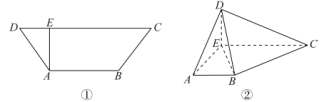
(1)若點![]() 為棱
為棱![]() 上任意一點,證明:平面
上任意一點,證明:平面![]() 平面
平面![]() .
.
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得三棱錐
,使得三棱錐![]() 的體積為
的體積為![]() ?若存在,確定
?若存在,確定![]() 點的位置;若不存在,請說明理由.
點的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為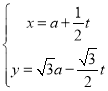 (
(![]() 為參數,
為參數,![]() ).在以坐標原點為極點、
).在以坐標原點為極點、![]() 軸的非負半軸為極軸的極坐標系中,曲線
軸的非負半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若點![]() 在直線
在直線![]() 上,求直線
上,求直線![]() 的極坐標方程;
的極坐標方程;
(2)已知![]() ,若點
,若點![]() 在直線
在直線![]() 上,點
上,點![]() 在曲線
在曲線![]() 上,且
上,且![]() 的最小值為
的最小值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2017年1月至2019年12月期間月接待游客量(單位:萬人)的數據,繪制了下面的折線圖.根據該折線圖,下列結論正確的是( )
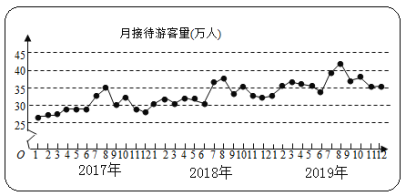
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位數為30
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 是拋物線
是拋物線![]() 上的兩個不同的點,
上的兩個不同的點,![]() 是坐標原點,若直線
是坐標原點,若直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
A.![]()
B.以![]() 為直徑的圓面積的最小值為
為直徑的圓面積的最小值為![]()
C.直線![]() 過拋物線
過拋物線![]() 的焦點
的焦點
D.點![]() 到直線
到直線![]() 的距離不大于
的距離不大于![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
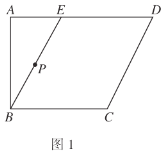
【題目】如圖1,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的點,
上的點,![]() ,
,![]() 為
為![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如圖2.
,如圖2.
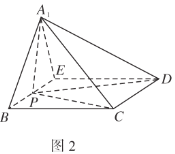
(1)求證:平面![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上,當直線
上,當直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com