
【題目】某商家在某一天統計前5名顧客掃微信紅包所得金額分別為5.9元,5.7元,4.7元,3.3元,2.1元,商家從這5名顧客中隨機抽取3人贈送禮品.
(Ⅰ)求獲得禮品的3人中恰好有2人的紅包超過5元的概率;
(Ⅱ)商家統計一周內每天使用微信支付的人數![]() 與每天的凈利潤
與每天的凈利潤![]() (單位:元),得到如下表:
(單位:元),得到如下表:
| 12 | 16 | 22 | 25 | 26 | 29 | 30 |
| 60 | 100 | 210 | 240 | 150 | 270 | 330 |
根據表中數據用最小二乘法求![]() 與
與![]() 的回歸方程
的回歸方程![]() (
(![]() ,
,![]() 的計算結果精確到小數點后第二位)并估計使用微信支付的人數增加到36人時,商家當天的凈利潤為多少(計算結果精確到小數點后第二位)?
的計算結果精確到小數點后第二位)并估計使用微信支付的人數增加到36人時,商家當天的凈利潤為多少(計算結果精確到小數點后第二位)?
參考數據及公式:
①![]() ,
,![]() ;
;![]() ;
;![]()
②回歸方程:![]() (其中
(其中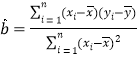 ,
,![]() )
)
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線
為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且設定點
兩點,且設定點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定橢圓![]() :
:![]() ,稱圓心在原點
,稱圓心在原點![]() ,半徑為
,半徑為![]() 的圓是橢圓
的圓是橢圓![]() 的“準圓”.若橢圓
的“準圓”.若橢圓![]() 的一個焦點為
的一個焦點為![]() ,其短軸上的一個端點到
,其短軸上的一個端點到![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程和其“準圓”方程;
的方程和其“準圓”方程;
(2)設橢圓短軸的一個端點為![]() ,長軸的一個端點為
,長軸的一個端點為![]() ,點
,點![]() 是“準圓”上一動點,求三角形
是“準圓”上一動點,求三角形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線的對稱軸為坐標軸,頂點是坐標原點,準線方程為![]() ,直線
,直線![]() 與拋物線相交于不同的
與拋物線相交于不同的![]() ,
, ![]() 兩點.
兩點.
(1)求拋物線的標準方程;
(2)如果直線![]() 過拋物線的焦點,求
過拋物線的焦點,求![]() 的值;
的值;
(3)如果![]() ,直線
,直線![]() 是否過一定點,若過一定點,求出該定點;若不過一定點,試說明理由.
是否過一定點,若過一定點,求出該定點;若不過一定點,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某地區鄉居民人民幣儲蓄存款(年底余額)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
時間代號x | 1 | 2 | 3 | 4 | 5 | 6 |
儲蓄存款y(千億元) | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求關于x的回歸方程![]() ,并預測該地區2019年的人民幣儲蓄存款(用最簡分數作答).
,并預測該地區2019年的人民幣儲蓄存款(用最簡分數作答).
(2)在含有一個解釋變量的線性模型中,![]() 恰好等于相關系數r的平方,當
恰好等于相關系數r的平方,當![]() 時,認為線性冋歸模型是有效的,請計算
時,認為線性冋歸模型是有效的,請計算![]() 并且評價模型的擬合效果(計算結果精確到0.001).
并且評價模型的擬合效果(計算結果精確到0.001).
附:
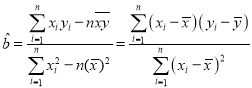 ,
,
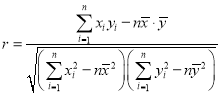
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正四棱柱![]() ,中,
,中,![]() .
.

(1)求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(2)若![]() 是線段
是線段![]() 上(不含線段的兩端點)的一個動點,請提出一個與三棱錐體積有關的數學問題(注:三棱錐需以點
上(不含線段的兩端點)的一個動點,請提出一個與三棱錐體積有關的數學問題(注:三棱錐需以點![]() 和已知正四棱柱八個頂點中的三個為頂點構成);并解答所提出的問題.
和已知正四棱柱八個頂點中的三個為頂點構成);并解答所提出的問題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】再直角坐標系中,定義兩點![]() ,
,![]() 間的“直角距離”為
間的“直角距離”為![]() ,現有下列命題:
,現有下列命題:
①若![]() ,
,![]() 是
是![]() 軸上兩點,則
軸上兩點,則![]()
②已知![]() ,
,![]() ,則
,則![]() 為定值
為定值
③原點![]() 到直線
到直線![]() 上任一點
上任一點![]() 的直角距離
的直角距離![]() 的最小值為
的最小值為![]()
④設![]() 且
且![]() ,
,![]() ,若點
,若點![]() 是在過
是在過![]() 與
與![]() 的直線上,且點
的直線上,且點![]() 到點
到點![]() 與
與![]() 的“直角距離”之和等于
的“直角距離”之和等于![]() ,那么滿足條件的點
,那么滿足條件的點![]() 只有
只有![]() 個.
個.
其中的真命題是____________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為弘揚中華傳統文化,某校組織高一年級學生到古都西安游學.在某景區,由于時間關系,每個班只能在甲、乙、丙三個景點中選擇一個游覽.高一![]() 班的
班的![]() 名同學決定投票來選定游覽的景點,約定每人只能選擇一個景點,得票數高于其它景點的入選.據了解,在甲、乙兩個景點中有
名同學決定投票來選定游覽的景點,約定每人只能選擇一個景點,得票數高于其它景點的入選.據了解,在甲、乙兩個景點中有![]() 人會選擇甲,在乙、丙兩個景點中有
人會選擇甲,在乙、丙兩個景點中有![]() 人會選擇乙.那么關于這輪投票結果,下列說法正確的是
人會選擇乙.那么關于這輪投票結果,下列說法正確的是
①該班選擇去甲景點游覽;
②乙景點的得票數可能會超過![]() ;
;
③丙景點的得票數不會比甲景點高;
④三個景點的得票數可能會相等.
A. ①② B. ①③ C. ②④ D. ③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b是異面直線,給出下列結論:
①一定存在平面![]() ,使直線
,使直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ;
;
②一定存在平面![]() ,使直線
,使直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ;
;
③一定存在無數個平面![]() ,使直線b與平面
,使直線b與平面![]() 交于一個定點,且直線
交于一個定點,且直線![]() 平面
平面![]() .
.
則所有正確結論的序號為( )
A.②③B.①③C.①②D.①②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com