
【題目】設橢圓E: ![]() (a>b>0),其長軸長是短軸長的
(a>b>0),其長軸長是短軸長的 ![]() 倍,過焦點且垂直于x軸的直線被橢圓截得的弦長為2
倍,過焦點且垂直于x軸的直線被橢圓截得的弦長為2 ![]() .
.
(1)求橢圓E的方程;
(2)設過右焦點F2且與x軸不垂直的直線l交橢圓E于P,Q兩點,在線段OF2(O為坐標原點)上是否存在點M(m,0),使得以MP,MQ為鄰邊的平行四邊形是菱形?若存在,求出m的取值范圍;若不存在,請說明理由.
【答案】
(1)解:不妨設焦點的坐標是(c,0),
則過焦點且垂直于x軸的直線與橢圓的交點坐標為(c,y0),
代入 ![]() 可得,y0=
可得,y0= ![]() ,
,
因為過焦點且垂直于x軸的直線被橢圓截得的弦長為2 ![]() ,
,
所以 ![]() ,
,
由題意得,a= ![]() b,代入上式解得:a=2
b,代入上式解得:a=2 ![]() 、b=
、b= ![]() ,
,
故所求橢圓方程為 ![]()
(2)解:假設在線段OF2上存在點M(m,0)( ![]() )滿足條件,
)滿足條件,
∵直線與x軸不垂直,
∴設直線l的方程為 ![]() .
.
設P(x1,y1),Q(x2,y2),
由 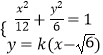 ,可得
,可得 ![]() .
.
則 ![]() ,
, ![]() .
.
∴ ![]() ,
, ![]() ,其中x2﹣x1≠0,
,其中x2﹣x1≠0,
∵以MP,MQ為鄰邊的平行四邊形是菱形,
∴ ![]() .
.
∴(x1+x2﹣2m)(x2﹣x1)+(y1+y2)(y2﹣y1)=0.
∴x1+x2﹣2m+k(y1+y2)=0.
∴ ![]() .
.
化簡得 ![]() =
= ![]() (k≠0),
(k≠0),
則 ![]()
在線段OF2上存在點M(m,0)符合條件,且 ![]()
【解析】(1)由題意先求出直線與橢圓的交點坐標,再列出方程求出a、b的值,代入橢圓方程即可;(2)先假設存在點M(m,0)( ![]() )滿足條件,由點斜式設出直線l的方程,以及P、Q的坐標,將直線方程代入橢圓方程化簡后,利用韋達定理、菱形的等價條件、向量知識,可求出m的范圍,再進行判斷.
)滿足條件,由點斜式設出直線l的方程,以及P、Q的坐標,將直線方程代入橢圓方程化簡后,利用韋達定理、菱形的等價條件、向量知識,可求出m的范圍,再進行判斷.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)為定義在R上的奇函數,且當x>0時,f(x)=1﹣x2 .
(1)求函數f(x)的解析式;
(2)作出函數f(x)的圖象.
(3)若函數f(x)在區間[a,a+1]上單調,直接寫出實數a的取值范圍.(不必寫出演算過程)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ex+x﹣2,g(x)=lnx+x2﹣3,若實數a,b滿足f(a)=0,g(b)=0,則( )
A.0<g(a)<f(b)
B.f(b)<g(a)<0
C.f(b)<0<g(a)
D.g(a)<0<f(b)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在“出彩中國人”的一期比賽中,有6位歌手(1~6)登臺演出,由現場的百家大眾媒體投票選出最受歡迎的出彩之星,各家媒體獨立地在投票器上選出3位出彩候選人,其中媒體甲是1號歌手的歌迷,他必選1號,另在2號至6號中隨機的選2名;媒體乙不欣賞2號歌手,他必不選2號;媒體丙對6位歌手的演唱沒有偏愛,因此在1至6號歌手中隨機的選出3名.
(1)求媒體甲選中3號且媒體乙未選中3號歌手的概率;
(2)X表示3號歌手得到媒體甲、乙、丙的票數之和,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=alnx+(x﹣c)|x﹣c|,a<0,c>0.
(1)當a=﹣ ![]() ,c=
,c= ![]() 時,求函數f(x)的單調區間;
時,求函數f(x)的單調區間;
(2)當c= ![]() +1時,若f(x)≥
+1時,若f(x)≥ ![]() 對x∈(c,+∞)恒成立,求實數a的取值范圍;
對x∈(c,+∞)恒成立,求實數a的取值范圍;
(3)設函數f(x)的圖象在點P(x1 , f(x1))、Q(x2 , f(x2))兩處的切線分別為l1、l2 . 若x1= ![]() ,x2=c,且l1⊥l2 , 求實數c的最小值.
,x2=c,且l1⊥l2 , 求實數c的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com