
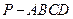
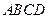
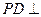
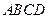
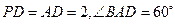 ,
,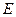 、
、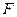 分別為
分別為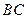 、
、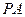 的中點(diǎn)。
的中點(diǎn)。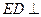 平面
平面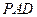 ;
;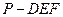 的體積;
的體積;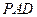 與平面
與平面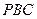 所成的銳二面角大小的余弦值。
所成的銳二面角大小的余弦值。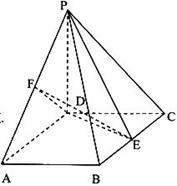
 (3)
(3)

 ,又
,又 ,
, ------------ 2分
------------ 2分 平面
平面 ,
, , ------------3分
, ------------3分 ,
, 平面PAD。 ------------4分
平面PAD。 ------------4分 ,
, , ------5分
, ------5分 --------8分
--------8分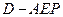 ,
,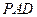 的一個(gè)法向量為
的一個(gè)法向量為
 ,
,
 ,
,
 得
得 ----------11分
----------11分 --------13分
--------13分 平面PAD與平面PBC所成的銳二面角大小的余弦值為
平面PAD與平面PBC所成的銳二面角大小的余弦值為 -------14分
-------14分 平面
平面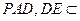 平面
平面 ,
, 平面
平面 平面
平面 -------9分
-------9分
 平面
平面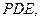 又
又 平面
平面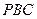
 平面
平面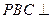 平面
平面 --------10分
--------10分 就是平面
就是平面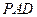 與平面
與平面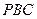 所成二面角的平面角 ---------12分
所成二面角的平面角 ---------12分 在
在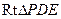 中,
中,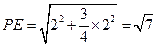
 --------14分
--------14分

 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
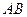 是圓柱體
是圓柱體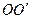 的一條母線,
的一條母線,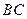 過底面圓的圓心
過底面圓的圓心 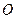 ,
,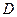 是圓
是圓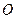 上不與點(diǎn)
上不與點(diǎn) 、
、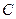 重合的任意一點(diǎn),已知棱
重合的任意一點(diǎn),已知棱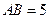 ,
, 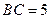 ,
,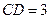 .
.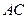 與平面
與平面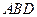 所成的角的大小;
所成的角的大小; 繞母線
繞母線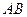 轉(zhuǎn)動(dòng)一周,求
轉(zhuǎn)動(dòng)一周,求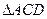 的三邊在旋 轉(zhuǎn)過程中所圍成的幾何體的體積.
的三邊在旋 轉(zhuǎn)過程中所圍成的幾何體的體積.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
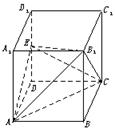
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題

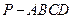
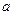
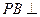 平面
平面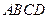 ,M、N分別是AB、PC的中點(diǎn)。
,M、N分別是AB、PC的中點(diǎn)。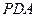 與平面
與平面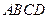 成
成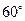 的二面角,
的二面角,查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
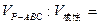 __________
__________查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.27π | B.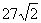 π π |
C.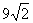 π π | D.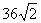 π π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
 與球O有且僅有一公共點(diǎn)P,從直線
與球O有且僅有一公共點(diǎn)P,從直線 出發(fā)的兩個(gè)半平面截球O的兩個(gè)截面圓O1和圓O2的半徑1和2,若這兩個(gè)半平面
出發(fā)的兩個(gè)半平面截球O的兩個(gè)截面圓O1和圓O2的半徑1和2,若這兩個(gè)半平面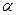 ,
, 所成二面角為1200,則球O的表面積為 。
所成二面角為1200,則球O的表面積為 。查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com