
①tanA·cotB=1 ②0<sinA+sinB≤![]() ③sin2A+cos2B=1 ④cos2A+cos2B=sin2C
③sin2A+cos2B=1 ④cos2A+cos2B=sin2C
A.①③ B.②④ C.①④ D.②③
解析:∵tan![]() =tan
=tan![]() =tan(90°-
=tan(90°-![]() )=cot
)=cot![]() =
=![]() =sinC=2sin
=sinC=2sin![]() cos
cos![]() ,
,
∴1=2sin2![]() .∴1-2sin2
.∴1-2sin2![]() =cosC=0.
=cosC=0.
∴C=90°.∴A+B=90°.
∴tanA·cotB=tanA·cot(90°-A)=tanA·tanA=tan2A=1不一定成立,
∴①錯誤.
∵sin2A+cos2B=sin2A+cos2(90°-B)=sin2A+sin2B=1不一定成立,
∴③錯.
∵0<sinA+sinB=sinA+sin(90°-A)=sinA+cosA=![]() sin(A+45°)≤
sin(A+45°)≤![]() ,
,
∴②正確.
∵cos2A+cos2B=cos2A+cos2(90°-A)=cos2A+sin2A=1=sin2C.
∴④正確.故選擇B.
答案:B


科目:高中數學 來源: 題型:
| AD |
| BC |
| AH |
| HD |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:南通高考密卷·數學(理) 題型:013
在△ABC中,已知三邊a,b,c成等差數列,且有sinB+cosB=t,則t的取值范圍是
[ ]
 )
) )
) ,+∞)
,+∞)查看答案和解析>>
科目:高中數學 來源:上杭一中、武平一中、長汀一中、漳平一中2006-2007學年第一學期高三期末考數學試題(理) 題型:044
在△ABC中,已知B(-3,0),C(3,0),D為線段BC上一點,![]() 是△ABC的垂心,且
是△ABC的垂心,且![]() .
.
(1)求點H的軌跡M的方程;
(2)若過C點且斜率為![]() 的直線與軌跡M交于點P,點Q(t,0)是x軸上任意一點,
的直線與軌跡M交于點P,點Q(t,0)是x軸上任意一點,
求:當△CPQ為銳角三角形時t的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2004年江蘇省無錫市高三調研數學試卷(解析版) 題型:解答題
 ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直線與軌跡M交于點P,點Q(t,0)是x軸上任意一點,求當△CPQ為銳角三角形時t的取值范圍.
的直線與軌跡M交于點P,點Q(t,0)是x軸上任意一點,求當△CPQ為銳角三角形時t的取值范圍.查看答案和解析>>
科目:高中數學 來源:江蘇省陸慕高級中學09-10學年高二上學期第一次測試 題型:解答題
在△ABC中,已知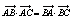 .
.
(Ⅰ) 求證: | |=|
|=| |;
|;
(Ⅱ) 若| +
+ |=|
|=| -
- |=
|= ,求|
,求| -t
-t |的最小值以及相應的t的值.
|的最小值以及相應的t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com