
【題目】已知函數(shù)![]() ,定義函數(shù)
,定義函數(shù) ,給出下列命題:①
,給出下列命題:①![]() ;②函數(shù)
;②函數(shù)![]() 是奇函數(shù);③當
是奇函數(shù);③當![]() 時,若
時,若![]() ,
,![]() ,總有
,總有![]() 成立,其中所有正確命題的序號是( )
成立,其中所有正確命題的序號是( )
A.②B.①②C.③D.②③
【答案】D
【解析】
①取![]() ,可得出當
,可得出當![]() 時,
時,![]() ,從而可判斷出命題①的正誤;利用定義判斷函數(shù)
,從而可判斷出命題①的正誤;利用定義判斷函數(shù)![]() 的奇偶性,可判斷出命題②的正誤;判斷出函數(shù)
的奇偶性,可判斷出命題②的正誤;判斷出函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)性,并設
上的單調(diào)性,并設![]() ,由題意得出正數(shù)的絕對值較大,再結合函數(shù)
,由題意得出正數(shù)的絕對值較大,再結合函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)性可判斷出命題③的正誤.
上的單調(diào)性可判斷出命題③的正誤.
對于命題①,取![]() 時,當
時,當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,此時
,此時![]() ,但
,但![]() ,則
,則![]() ,命題①錯誤;
,命題①錯誤;
對于命題②,函數(shù)![]() 的定義域為
的定義域為![]() ,關于原點對稱,
,關于原點對稱,
當![]() 時,
時,![]() ,
,
則![]() ;
;
當![]() 時,
時,![]() ,則
,則![]() .
.
所以,函數(shù)![]() 為奇函數(shù),命題②正確;
為奇函數(shù),命題②正確;
對于命題③,由②知,函數(shù)![]() 為奇函數(shù),當
為奇函數(shù),當![]() 時,
時,![]() 在
在![]() 上為減函數(shù),
上為減函數(shù),
![]() ,設
,設![]() ,又
,又![]() ,則
,則![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,所以,
,所以,![]() ,命題③正確.
,命題③正確.
因此,正確命題的序號為②③.
故選:D.


科目:高中數(shù)學 來源: 題型:
【題目】某汽車公司最近研發(fā)了一款新能源汽車,并在出廠前對100輛汽車進行了單次最大續(xù)航里程的測試。現(xiàn)對測試數(shù)據(jù)進行分析,得到如圖所示的頻率分布直方圖:
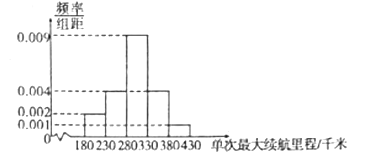
(1)估計這100輛汽車的單次最大續(xù)航里程的平均值(同一組中的數(shù)據(jù)用該組區(qū)間的中點值代表).
(2)根據(jù)大量的汽車測試數(shù)據(jù),可以認為這款汽車的單次最大續(xù)航里程![]() 近似地服從正態(tài)分布
近似地服從正態(tài)分布![]() ,經(jīng)計算第(1)問中樣本標準差
,經(jīng)計算第(1)問中樣本標準差![]() 的近似值為50。用樣本平均數(shù)
的近似值為50。用樣本平均數(shù)![]() 作為
作為![]() 的近似值,用樣本標準差
的近似值,用樣本標準差![]() 作為
作為![]() 的估計值,現(xiàn)任取一輛汽車,求它的單次最大續(xù)航里程恰在250千米到400千米之間的概率.
的估計值,現(xiàn)任取一輛汽車,求它的單次最大續(xù)航里程恰在250千米到400千米之間的概率.
參考數(shù)據(jù):若隨機變量服從正態(tài)分布![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
(3)某汽車銷售公司為推廣此款新能源汽車,現(xiàn)面向意向客戶推出“玩游戲,送大獎”活動,客戶可根據(jù)拋擲硬幣的結果,操控微型遙控車在方格圖上行進,若遙控車最終停在“勝利大本營”,則可獲得購車優(yōu)惠券3萬元。已知硬幣出現(xiàn)正、反面的概率都是0.5方格圖上標有第0格、第1格、第2格、…、第20格。遙控車開始在第0格,客戶每擲一次硬幣,遙控車向前移動一次。若擲出正面,遙控車向前移動一格(從![]() 到
到![]() )若擲出反面遙控車向前移動兩格(從
)若擲出反面遙控車向前移動兩格(從![]() 到
到![]() ),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時,游戲結束。設遙控車移到第
),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時,游戲結束。設遙控車移到第![]() 格的概率為P試證明
格的概率為P試證明![]() 是等比數(shù)列,并求參與游戲一次的顧客獲得優(yōu)惠券金額的期望值。
是等比數(shù)列,并求參與游戲一次的顧客獲得優(yōu)惠券金額的期望值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設橢圓M:![]() 的左頂點為
的左頂點為![]() 、中心為
、中心為![]() ,若橢圓M過點
,若橢圓M過點![]() ,且
,且![]()
![]() .
.
(1)求橢圓M的方程;
(2)若△APQ的頂點Q也在橢圓M上,試求△APQ面積的最大值;
(3)過點![]() 作兩條斜率分別為
作兩條斜率分別為![]() 的直線交橢圓M于
的直線交橢圓M于![]() 兩點,且
兩點,且![]() ,求證:直線
,求證:直線![]() 恒過一個定點.
恒過一個定點.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)![]() 的定義域
的定義域![]() 恰是不等式
恰是不等式![]() 的解集,其值域為
的解集,其值域為![]() ,函數(shù)
,函數(shù)![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() .
.
(1)求![]() 定義域
定義域![]() 和值域
和值域![]() ;
;
(2)試用單調(diào)性的定義法解決問題:若存在實數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,![]() 上單調(diào)遞增,求實數(shù)
上單調(diào)遞增,求實數(shù)![]() 的取值范圍并用
的取值范圍并用![]() 表示
表示![]() ;
;
(3)是否存在實數(shù)![]() ,使
,使![]() 成立?若存在,求實數(shù)
成立?若存在,求實數(shù)![]() 的取值范圍,若不存在,說明理由.
的取值范圍,若不存在,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com