
【題目】已知函數![]() .
.
(1)當![]() 時,判斷
時,判斷![]() 的單調性;
的單調性;
(2)若![]() 在
在![]() 上為單調增函數,求實數
上為單調增函數,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)在![]() 上為增函數;(2)
上為增函數;(2)![]() .
.
【解析】試題分析:(1)當![]() 時,對函數求導后因式分解,根據導數與單調性的知識可寫出函數的單調區間.(2)當
時,對函數求導后因式分解,根據導數與單調性的知識可寫出函數的單調區間.(2)當![]() 時,可判斷函數導數恒為非負數,函數遞增符合題意.當
時,可判斷函數導數恒為非負數,函數遞增符合題意.當![]() 和
和![]() 時,利用函數的二階導數判斷出不符合題意.故
時,利用函數的二階導數判斷出不符合題意.故![]() .
.
試題解析:
(1)當![]() 時,
時, 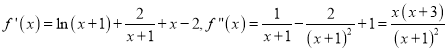 ,所以
,所以![]() 在
在![]() 上為減函數,在
上為減函數,在 ![]() 上為增函數,即
上為增函數,即![]() ,從而可得:
,從而可得: ![]() 在定義域
在定義域 ![]() 上為增函數.
上為增函數.
(2) ①當![]() 時,由于
時,由于![]() ,所以滿足
,所以滿足![]() 在
在 ![]() 上為單調增函數,即
上為單調增函數,即![]() ;
;
②當![]() 時,
時, ![]()
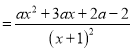 ,由方程
,由方程![]() 的判別式:
的判別式: ![]() ,所以方程有兩根
,所以方程有兩根![]() ,且由
,且由![]() 知
知![]() ,
, ![]() 在
在![]() 上為減函數,由
上為減函數,由![]() 可知,在
可知,在![]() 時,
時, ![]() ,這與
,這與 ![]() 在
在![]() 上為單調增函數相矛盾. ③ 當
上為單調增函數相矛盾. ③ 當![]() 時,
時, ![]()
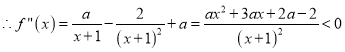 ,
, ![]() 在
在![]() 上為減函數,由
上為減函數,由![]() 可知,在
可知,在![]() 時,
時, ![]() ,這與
,這與 ![]() 在
在![]() 上為單調增函數也是相矛盾. 綜上所述:實數
上為單調增函數也是相矛盾. 綜上所述:實數![]() 的取值范圍是
的取值范圍是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某社區超市購進了A,B,C,D四種新產品,為了解新產品的銷售情況,該超市隨機調查了15位顧客(記為![]() )購買這四種新產品的情況,記錄如下(單位:件):
)購買這四種新產品的情況,記錄如下(單位:件):
顧 客 產 品 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A | 1 | 1 | 1 | 1 | 1 | ||||||||||
B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
D | 1 | 1 | 1 | 1 | 1 | 1 |
(Ⅰ)若該超市每天的客流量約為300人次,一個月按30天計算,試估計產品A的月銷售量(單位:件);
(Ⅱ)為推廣新產品,超市向購買兩種以上(含兩種)新產品的顧客贈送2元電子紅包.現有甲、乙、丙三人在該超市購物,記他們獲得的電子紅包的總金額為X,
求隨機變量X的分布列和數學期望;
(Ⅲ)若某顧客已選中產品B,為提高超市銷售業績,應該向其推薦哪種新產品?(結果不需要證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() ,離心率
,離心率![]() ,它的長軸長等于圓
,它的長軸長等于圓![]() 的直徑.
的直徑.
(1)求橢圓 ![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,是否存在定點
兩點,是否存在定點![]() ,使得以
,使得以![]() 為直徑的圓經過這個定點,若存在,求出定點
為直徑的圓經過這個定點,若存在,求出定點![]() 的坐標;若不存在,請說明理由?
的坐標;若不存在,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中, ![]() ,頂點
,頂點![]() 在底面
在底面 ![]() 上的射影恰為點
上的射影恰為點 ![]() ,且
,且![]() .
.

(1)求棱 ![]() 與
與![]() 所成的角的大小;
所成的角的大小;
(2)在棱 ![]() 上確定一點
上確定一點![]() ,使
,使![]() ,并求出二面角
,并求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
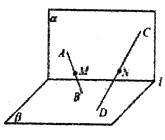
【題目】如圖,平面![]() 平面
平面![]() ,
, ![]() 直線
直線![]() ,
, ![]() 是
是![]() 內不同的兩點,
內不同的兩點, ![]() 是
是![]() 內不同的兩點,且
內不同的兩點,且![]() 直線
直線![]() 上
上![]() 分別是線段
分別是線段![]() 的中點,下列判斷正確的是( )
的中點,下列判斷正確的是( )
A. 當![]() 時,
時, ![]() 兩點不可能重合
兩點不可能重合
B. ![]() 兩點可能重合,但此時直線
兩點可能重合,但此時直線![]() 與
與![]() 不可能相交
不可能相交
C. 當![]() 與
與![]() 相交,直線
相交,直線![]() 平行于
平行于![]() 時,直線
時,直線![]() 可以與
可以與![]() 相交
相交
D. 當![]() 是異面直線時,直線
是異面直線時,直線![]() 可能與
可能與![]() 平行
平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的極坐標方程是![]() .以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線l的參數方程是:
.以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線l的參數方程是: 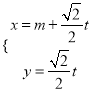 (
(![]() 是參數).
是參數).
(Ⅰ)將曲線C的極坐標方程化為直角坐標方程,將直線![]() 的參數方程化為普通方程;
的參數方程化為普通方程;
(Ⅱ)若直線l與曲線C相交于A、B兩點,且![]() ,試求實數m的值.
,試求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com