
 ,cos(α+β)=-
,cos(α+β)=- ,且α,β∈(0,
,且α,β∈(0, ),則cos(α-β)的值等于( )
),則cos(α-β)的值等于( )


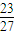
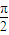 ),∴2α∈(0,π).
),∴2α∈(0,π). ,∴cos2α=2cos2α-1=-
,∴cos2α=2cos2α-1=- ,∴sin2α=
,∴sin2α=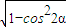 =
=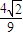 ,
,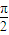 ),∴α+β∈(0,π),
),∴α+β∈(0,π),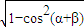
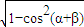 =
=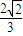 ,
, )×(-
)×(- )+
)+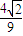 ×
×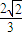
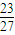 .
.

 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:
| 3 | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
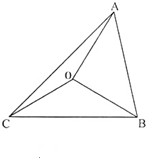 (2011•杭州一模)已知點O為△ABC的外心,角A,B,C的對邊分別滿足a,b,c,
(2011•杭州一模)已知點O為△ABC的外心,角A,B,C的對邊分別滿足a,b,c,| OA |
| OB |
| OC |
| 0 |
| CO |
| AB |
| BO |
| CA |
| b2+c2 |
| a2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 4 |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| m |
| n |
| AP |
| AO |
| AC |
| PA |
| PB |
| PC |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com