
【題目】數列{an}中,已知a1= ![]() ,an+1=
,an+1= ![]() .
.
(1)證明:an<an+1< ![]() ;
;
(2)證明:當n≥2時,( ![]() )
) ![]() <2.
<2.
【答案】
(1)證明:由 ![]() ,得
,得 ![]() ,即0≤an≤1.
,即0≤an≤1.
∴an+1= ![]() =
= ![]() ,
,
又a1= ![]() ≠0,且
≠0,且 ![]() ,∴0
,∴0 ![]() .
.
∴ ![]() >0.
>0.
即 ![]()
(2)證明:當n=2時, ![]() ,
,
又∵ ![]() ,
,
∴ ![]() .
.
即當n=2時, ![]() 成立,
成立,
當n=k時, ![]() 成立,即
成立,即 ![]() 成立,
成立,
當n=k+1時, ![]() =
= ![]() .
.
∵an+1>an,∴ak+1>ak
∴ ![]() .
.
則 ![]() =
= ![]() ,
,
∴當n=k+1時, ![]() 也成立,
也成立,
∴當n≥2時, ![]() 成立
成立
【解析】(1)由已知a1= ![]() ,an+1=
,an+1= ![]() ,即可得到
,即可得到 ![]() ,又0
,又0 ![]() ,進一步得到
,進一步得到 ![]() ,則結論an<an+1<
,則結論an<an+1< ![]() 可證;(2)首先證當n=2時,
可證;(2)首先證當n=2時, ![]() 成立,即當n=k時,
成立,即當n=k時, ![]() 成立,當n=k+1時,ak+1>ak , 則
成立,當n=k+1時,ak+1>ak , 則 ![]() =
= ![]() ,則結論當n≥2時,(
,則結論當n≥2時,( ![]() )
) ![]() <2可證.
<2可證.
【考點精析】關于本題考查的數列的通項公式,需要了解如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式才能得出正確答案.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】通過隨機詢問110名性別不同的大學生是否愛好某項運動,得到如下的列聯表:
男 | 女 | 合 計 | |
愛好 | 40 | 20 | 60 |
不愛好 | 20 | 30 | 50 |
合 計 | 60 | 50 | 110 |
根據上述數據能得出的結論是( )
(參考公式與數據:X2= ![]() .當X2>3.841時,有95%的把握說事件A與B有關;當X2>6.635時,有99%的把握說事件A與B有關; 當X2<3.841時認為事件A與B無關.)
.當X2>3.841時,有95%的把握說事件A與B有關;當X2>6.635時,有99%的把握說事件A與B有關; 當X2<3.841時認為事件A與B無關.)
A.有99%的把握認為“愛好該項運動與性別有關”
B.有99%的把握認為“愛好該項運動與性別無關”
C.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
D.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,△ABC是邊長為2的正三角形,∠PCA=90°,E,H分別為AP,AC的中點,AP=4,BE=![]() .
.
(Ⅰ)求證:AC⊥平面BEH;
(Ⅱ)求直線PA與平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,∠BAC=10°,∠ACB=30°,將直線BC繞AC旋轉得到B1C,直線AC繞AB旋轉得到AC1 , 則在所有旋轉過程中,直線B1C與直線AC1所成角的取值范圍為 . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A1 , A2 , …,An(n≥4)為集合S={1,2,…,n}的n個不同子集,為了表示這些子集,作n行n列的數陣,規定第i行第j列的數為: ![]() .則下列說法中,錯誤的是( )
.則下列說法中,錯誤的是( ) 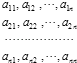
A.數陣中第一列的數全是0當且僅當A1=
B.數陣中第n列的數全是1當且僅當An=S
C.數陣中第j行的數字和表明集合Aj含有幾個元素
D.數陣中所有的n2個數字之和不超過n2﹣n+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交通管理部門為了解機動車駕駛員(簡稱駕駛員)對某新法規的知曉情況,對甲、乙、丙、丁四個社區做分層抽樣調查.假設四個社區駕駛員的總人數為N,其中甲社區有駕駛員96人.若在甲、乙、丙、丁四個社區抽取駕駛員的人數分別為12,21,25,43,則這四個社區駕駛員的總人數N為( )
A.101
B.808
C.1212
D.2012
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)經過點(2,
(a>b>0)經過點(2, ![]() )且離心率等于
)且離心率等于 ![]() ,點A,B分別為橢圓C的左右頂點,點P在橢圓C上.
,點A,B分別為橢圓C的左右頂點,點P在橢圓C上.
(1)求橢圓C的方程;
(2)M,N是橢圓C上非頂點的兩點,滿足OM∥AP,ON∥BP,求證:三角形MON的面積是定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com