
【題目】在直角坐標系xOy中,以O為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為ρsin(θ+ ![]() )=
)= ![]() .圓O的參數方程為
.圓O的參數方程為  (θ為參數,r>0).
(θ為參數,r>0).
(Ⅰ)求圓O的圓心的極坐標(ρ≥0,0≤θ<2π );
(Ⅱ)當r為何值時,圓O上的點到直線l的最大距離為2+ ![]() .
.
【答案】解:(Ⅰ)圓O的參數方程為 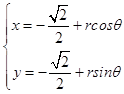 , 可得圓心為(
, 可得圓心為( ![]() ),
),
由ρ2=x2+y2 , 可得ρ=1,tanθ= ![]() =
= ![]() .
.
∴圓心的極坐標為(1, ![]() ).
).
(Ⅱ)直線l的極坐標方程ρsin(θ+ ![]() )=
)= ![]() 化為普通方程,可得
化為普通方程,可得 ![]() ρsinθ+
ρsinθ+ ![]() ρcosθ=
ρcosθ= ![]() ,即x+y﹣1=0,
,即x+y﹣1=0,
把參數方程 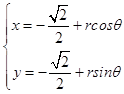 ,
,
由圓心到直線的距離公式d= 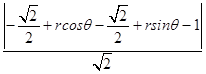 ,即d=
,即d= 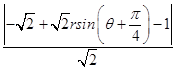 ,
,
當sin( ![]() )=﹣1時,圓O上的點到直線l的最大,即
)=﹣1時,圓O上的點到直線l的最大,即 ![]() =2+
=2+ ![]() ,
,
解得r=1
∴當r=1時,圓O上的點到直線l的最大距離為2+ ![]()
【解析】(Ⅰ)根據圓O的參數方程為 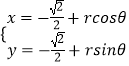 可得圓心為(
可得圓心為( ![]() ),根據ρ2=x2+y2 , 可得ρ=1,tanθ=
),根據ρ2=x2+y2 , 可得ρ=1,tanθ= ![]() =
= ![]() .可得圓心的極坐標.(Ⅱ)將直線l的極坐標方程ρsin(θ+
.可得圓心的極坐標.(Ⅱ)將直線l的極坐標方程ρsin(θ+ ![]() )=
)= ![]() 化為普通方程,然后把參數方程
化為普通方程,然后把參數方程 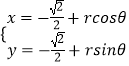 帶入圓心到直線的距離公式d,利用三角函數的有界限即可求.
帶入圓心到直線的距離公式d,利用三角函數的有界限即可求.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】若定義域為R的奇函數f(x)滿足f(1+x)=﹣f(x),則下列結論: ①f(x)的圖象關于點 ![]() 對稱;
對稱;
②f(x)的圖象關于直線 ![]() 對稱;
對稱;
③f(x)是周期函數,且2個它的一個周期;
④f(x)在區間(﹣1,1)上是單調函數.
其中正確結論的序號是 . (填上你認為所有正確結論的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正四面體P﹣ABC中,點M是棱PC的中點,點N是線段AB上一動點,且 ![]() ,設異面直線 NM 與 AC 所成角為α,當
,設異面直線 NM 與 AC 所成角為α,當 ![]() 時,則cosα的取值范圍是 .
時,則cosα的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點P在△ABC的BC邊所在的直線上從左到右運動,設△ABP與△ACP的外接圓面積之比為λ,當點P不與B,C重合時,( )
A.λ先變小再變大
B.當M為線段BC中點時,λ最大
C.λ先變大再變小
D.λ是一個定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A是單位圓O和x軸正半軸的交點,P,Q是圓O上兩點,O為坐標原點,∠AOP= ![]() ,∠AOQ=α,α∈[0,
,∠AOQ=α,α∈[0, ![]() ].
].
(1)若Q( ![]() ,
, ![]() ),求cos(α﹣
),求cos(α﹣ ![]() )的值;
)的值;
(2)設函數f(α)=sinα( ![]()
![]() ),求f(α)的值域.
),求f(α)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
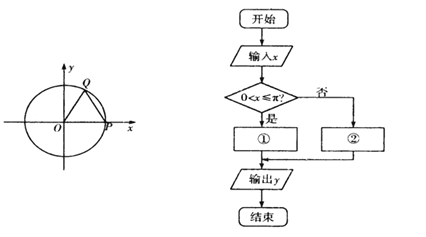
【題目】如圖,已知單位圓x2+y2=1與x軸正半軸交于點P,當圓上一動點Q從P出發沿逆時針方向旋轉一周回到P點后停止運動設OQ掃過的扇形對應的圓心角為xrad,當0<x<2π時,設圓心O到直線PQ的距離為y,y與x的函數關系式y=f(x)是如圖所示的程序框圖中的①②兩個關系式
(Ⅰ)寫出程序框圖中①②處的函數關系式;
(Ⅱ)若輸出的y值為2,求點Q的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合M={x|x<2},集合N={x|0<x<1},則下列關系中正確的是( )
A.M∪N=R
B.M∪RN=R
C.N∪RM=R
D.M∩N=M
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某服裝批發市場1-5月份的服裝銷售量![]() 與利潤
與利潤![]() 的統計數據如下表:
的統計數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
銷售量 | 3 | 6 | 4 | 7 | 8 |
利潤 | 19 | 34 | 26 | 41 | 46 |
(1)從這五個月的利潤中任選2個,分別記為![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知銷售量![]() 與利潤
與利潤![]() 大致滿足線性相關關系,請根據前4個月的數據,求出
大致滿足線性相關關系,請根據前4個月的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的利潤的估計數據與真實數據的誤差不超過2萬元,則認為得到的利潤的估計數據是理想的.請用表格中第5個月的數據檢驗由(2)中回歸方程所得的第5個月的利潤的估計數據是否理想.參考公式:  .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com