
【題目】筒車是我國古代發明的一種水利灌溉工具,明朝科學家徐光啟在《農政全書》中用圖畫描繪了筒車的工作原理(如圖1).因其經濟又環保,至今還在農業生產中得到使用(如圖2).假定在水流量穩定的情況下,筒車上的每一個盛水筒都做勻速圓周運動.因筒車上盛水筒的運動具有周期性,可以考慮利用三角函數模型刻畫盛水筒(視為質點)的運動規律.將筒車抽象為一個幾何圖形,建立直角坐標系(如圖3).設經過t秒后,筒車上的某個盛水筒![]() 從點P0運動到點P.由筒車的工作原理可知,這個盛水筒距離水面的高度H(單位:
從點P0運動到點P.由筒車的工作原理可知,這個盛水筒距離水面的高度H(單位: ![]() ),由以下量所決定:筒車轉輪的中心O到水面的距離h,筒車的半徑r,筒車轉動的角速度ω(單位:
),由以下量所決定:筒車轉輪的中心O到水面的距離h,筒車的半徑r,筒車轉動的角速度ω(單位: ![]() ),盛水筒的初始位置P0以及所經過的時間t(單位:
),盛水筒的初始位置P0以及所經過的時間t(單位:![]() ).已知r=3
).已知r=3![]() ,h=2
,h=2![]() ,筒車每分鐘轉動(按逆時針方向)1.5圈, 點P0距離水面的高度為3.5
,筒車每分鐘轉動(按逆時針方向)1.5圈, 點P0距離水面的高度為3.5![]() ,若盛水筒M從點P0開始計算時間,則至少需要經過_______
,若盛水筒M從點P0開始計算時間,則至少需要經過_______![]() 就可到達最高點;若將點
就可到達最高點;若將點![]() 距離水面的高度
距離水面的高度![]() 表示為時間
表示為時間![]() 的函數,則此函數表達式為_________.
的函數,則此函數表達式為_________.



圖1 圖2 圖3
【答案】![]()
![]()
【解析】
由題設條件求出初始位置![]() 與
與![]() 非負半軸的夾角,當
非負半軸的夾角,當![]() 第一次到達最高點時,求出所轉過的弧度,根據筒車每秒鐘轉動的弧度,求出第一次到達最高點的時間,即可得出第一空;
第一次到達最高點時,求出所轉過的弧度,根據筒車每秒鐘轉動的弧度,求出第一次到達最高點的時間,即可得出第一空;
由三角函數的定義得出動點![]() 的縱坐標,利用縱坐標求出點
的縱坐標,利用縱坐標求出點![]() 距離水面的高度
距離水面的高度![]() ,即可得出第二空.
,即可得出第二空.
因為點P0距離水面的高度為3.5![]() ,則開始時
,則開始時![]() 與
與![]() 非負半軸的夾角為
非負半軸的夾角為![]()
由題意可知,筒車每分鐘轉動(按逆時針方向)![]() ,即筒車每秒鐘轉動
,即筒車每秒鐘轉動![]()
當![]() 第一次到達最高點時,所轉過的弧度為
第一次到達最高點時,所轉過的弧度為![]() ,則所用時間為
,則所用時間為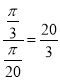
即若盛水筒M從點P0開始計算時間,則至少需要經過![]()
![]() 就可到達最高點;
就可到達最高點;
設![]() 與
與![]() 非負半軸的夾角為
非負半軸的夾角為![]() ,則
,則![]()
由三角函數的定義可知點![]() 的縱坐標為
的縱坐標為![]() ,
,![]()
則點![]() 距離水面的高度
距離水面的高度![]() 的函數為
的函數為![]() ,
,![]()
故答案為:![]() ;
;![]()


科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形,![]() 底面
底面![]() ,
,![]() 是棱
是棱![]() 的中點,且
的中點,且![]() ,
,![]() .
.

(1)求證:![]() 平面
平面![]() .
.
(2)求二面角![]() 的大小;
的大小;
(3)如果![]() 是棱
是棱![]() 的中點,求直線
的中點,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C的焦點在y軸上,焦點到準線的距離為2,且對稱軸為y軸.
(1)求拋物線C的標準方程;
(2)當拋物線C的焦點為![]() 時,過F作直線交拋物線于,A、B兩點,若直線OA,OB(O為坐標原點)分別交直線
時,過F作直線交拋物線于,A、B兩點,若直線OA,OB(O為坐標原點)分別交直線![]() 于M、N兩點,求
于M、N兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
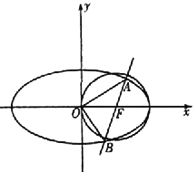
【題目】如圖,橢圓G的中心在坐標原點,其中一個焦點為圓F:x2+y2﹣2x=0的圓心,右頂點是圓F與x軸的一個交點.已知橢圓G與直線l:x﹣my﹣1=0相交于A、B兩點.
(I)求橢圓的方程;
(Ⅱ)求△AOB面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知2017年![]() 市居民平均家庭凈收入走勢圖(家庭凈收入=家庭總收入一家庭總支出),如圖所示,則下列說法錯誤的是( )
市居民平均家庭凈收入走勢圖(家庭凈收入=家庭總收入一家庭總支出),如圖所示,則下列說法錯誤的是( )

A. 2017年2月份![]() 市居國民的平均家庭凈收入最低
市居國民的平均家庭凈收入最低
B. 2017年4,5,6月份![]() 市居民的平均家庭凈收入比7、8、9月份的平均家庭凈收入波動小
市居民的平均家庭凈收入比7、8、9月份的平均家庭凈收入波動小
C. 2017年有3個月![]() 市居民的平均家庭凈收入低于4000元
市居民的平均家庭凈收入低于4000元
D. 2017年9、10、11、12月份平均家庭凈收入持續降低
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于點
于點![]() ,將
,將![]() 沿
沿![]() 折起,使
折起,使![]() ,連接
,連接![]() 、
、![]() ,得到如圖②所示的幾何體.
,得到如圖②所示的幾何體.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若點![]() 在線段
在線段![]() 上,直線
上,直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 作垂直于
作垂直于![]() 軸的直線與拋物線交于
軸的直線與拋物線交于![]() ,
,![]() 兩點,且以線段
兩點,且以線段![]() 為直徑的圓過點
為直徑的圓過點![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 為曲線
為曲線![]() :
:![]() 上的動點,求
上的動點,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】短道速滑隊組織6名隊員(包括賽前系列賽積分最靠前的甲乙丙三名隊員在內)參加冬奧會選拔賽,記“甲得第一名”為![]() ,“乙得第二名”為
,“乙得第二名”為![]() ,“丙得第三名”為
,“丙得第三名”為![]() ,若
,若![]() 是真命題,
是真命題,![]() 是假命題,
是假命題,![]() 是真命題,則選拔賽的結果為( )
是真命題,則選拔賽的結果為( )
A.甲得第一名、乙得第三名、丙得第二名
B.甲沒得第一名、乙沒得第二名、丙得第三名
C.甲得第一名、乙沒得第二名、丙得第三名
D.甲得第二名、乙得第一名、丙得第三名
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com