
分析 ①,當兩個側面是矩形且相鄰時,四棱柱是直四棱柱;當兩個側面是矩形且不相鄰時,四棱柱不是直四棱柱;
②,側面都是等腰三角形的三棱錐不一定是正三棱錐;
③,-2≤2x-3≤2⇒$\frac{1}{2}$≤x≤$\frac{5}{2}$,則f(2x-3)的定義域為[$\frac{1}{2}$,$\frac{5}{2}$],
④,函數y=f(-x)與y=f(x)的圖象關于直線x=0對稱,則函數y=f(1-x)=f(-(x-1))與y=f(x-1)的圖象關于直線x=1對稱
⑤,畫出函數的圖象,根據a,b,c互不相等,且f(a)=f(b)=f(c),我們令a<b<c,我們易根據對數的運算性質,及c的取值范圍得到abc的取值范圍
解答 解:對于①,當兩個側面是矩形且相鄰時,四棱柱是直四棱柱;當兩個側面是矩形且不相鄰時,四棱柱不是直四棱柱,故①錯;
對于②側面都是等腰三角形的三棱錐不一定是正三棱錐,
如圖所示,VA=VC=BC=AB,AC=VB時,不一定是正三棱錐,故錯;
對于③,∵-2≤2x-3≤2⇒$\frac{1}{2}$≤x≤$\frac{5}{2}$,則f(2x-3)的定義域為[$\frac{1}{2}$,$\frac{5}{2}$],故錯;
對于④,函數y=f(-x)與y=f(x)的圖象關于直線x=0對稱,則函數y=f(1-x)=f(-(x-1))與y=f(x-1)的圖象關于直線x=1對稱,故正確;
對于⑤,若a,b,c互不相等,且f(a)=f(b)=f(c),令a<b<c,則a•b=1,2<c<4,故2<abc<4,故正確;
故答案為:④⑤
點評 本題考查了命題真假的判定,涉及到了大量的基礎知識,屬于基礎題.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:選擇題
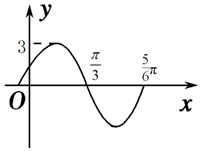 函數y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示,則( )
函數y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示,則( )| A. | f(x)的一個對稱中心為$(\frac{4π}{3},0)$ | B. | f(x)的圖象關于直線$x=-\frac{1}{12}π$ 對稱 | ||
| C. | f(x)在$[-π,-\frac{π}{2}]$上是增函數 | D. | f(x)的周期為$\frac{π}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $a+\frac{1}{b}>b+\frac{1}{a}$ | B. | $\frac{1}{{a{b^2}}}>\frac{1}{{{a^2}b}}$ | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | ab>b2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | 1 | C. | 4 | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 48 | B. | 62 | C. | 76 | D. | 90 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com