
【題目】已知函數![]() .
.
(1)若函數![]() 與
與![]() 的圖象恰好相切與點
的圖象恰好相切與點![]() ,求實數
,求實數![]() 的值;
的值;
(2)當![]() 時,
時, ![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)求證: ![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)見解析
(3)見解析
【解析】試題分析:(1)根據導數幾何意義得![]() ,即得實數
,即得實數![]() 的值;(2)利用分參法將不等式恒成立問題轉化為對應函數最值問題
的值;(2)利用分參法將不等式恒成立問題轉化為對應函數最值問題![]() (x>1)最大值,再利用導數研究函數
(x>1)最大值,再利用導數研究函數![]() 單調性:單調遞減,最后根據洛必達法則求最大值,即得實數
單調性:單調遞減,最后根據洛必達法則求最大值,即得實數![]() 的取值范圍(3)先根據和的關系轉化為對應項的關系:
的取值范圍(3)先根據和的關系轉化為對應項的關系: ![]() ,再利用(2)的結論
,再利用(2)的結論![]() ,令
,令![]() ,則代入放縮得證
,則代入放縮得證
試題解析:(1)![]()
所以![]()
(2)方法一:(分參)
即![]() 時,
時, ![]() ,
, ![]() 時,顯然成立;
時,顯然成立;
![]() 時,即
時,即![]()
令![]() ,則
,則
令![]() []
[]
![]()
![]() 即
即![]()
![]() 在
在![]() 上單調遞減
上單調遞減
![]()
故![]()
方法二:(先找必要條件)
注意到![]() 時,恰有
時,恰有![]()
令![]()
則
![]() 在
在![]() 恒成立的必要條件為
恒成立的必要條件為![]()
即![]()
下面證明:當![]() 時,
時, ![]()

令![]()
![]() 即
即![]()
![]() 在
在![]() 遞減,
遞減,
![]() 恒成立,即
恒成立,即![]() 也是充分條件,故有
也是充分條件,故有![]() .
.
(3)不妨設![]() 為
為![]() 前
前![]() 項和,則
項和,則![]()
要證原不等式,只需證![]()
而由(2)知:當![]() 時恒有
時恒有![]()
即![]() 當且僅當
當且僅當![]() 時取等號
時取等號
取![]() ,則
,則
即![]() 即
即![]()
即![]() 成立,從而原不等式獲證.
成立,從而原不等式獲證.


科目:高中數學 來源: 題型:
【題目】已知兩直線l1:x+8y+7=0和l2:2x+y﹣1=0.
(1)求l1與l2交點坐標;
(2)求過l1與l2交點且與直線x+y+1=0平行的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出如下幾個結論:①命題“x∈R,sinx+cosx=2”的否定是“x∈R,sinx+cosx≠2”;②命題“x∈R,sinx+ ![]() ≥2”的否定是“x∈R,sinx+
≥2”的否定是“x∈R,sinx+ ![]() <2”;③對于x∈(0,
<2”;③對于x∈(0, ![]() ),tanx+
),tanx+ ![]() ≥2;
≥2;
④x∈R,使sinx+cosx= ![]() .其中正確的為( )
.其中正確的為( )
A.③
B.③④
C.②③④
D.①②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,曲線![]() 的方程為
的方程為![]() .以坐標原點為極點,
.以坐標原點為極點, ![]() 軸的非負半軸為極軸,建立極坐標系,曲線
軸的非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的參數方程和曲線
的參數方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 在曲線
在曲線![]() 上,點
上,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面程序框圖的算法思路源于我國古代數學名著《九章算術》中的“更相減損術”,執行該程序框圖,若輸入的![]() 分別為14,18,則輸出的
分別為14,18,則輸出的![]() 為( )
為( )
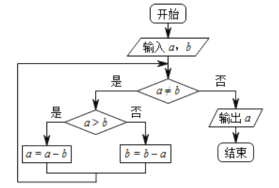
A. 0 B. 2 C. 4 D. 14
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校在2013年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組:第1組[160,165),第2組[165,170),第3組[170,175),第4組[175,180),第5組[180,85],得到的頻率分布直方圖如圖所示.
(1)求第3,4,5組的頻率;
(2)為了能選拔出最優秀的學生,該校決定在筆試成績高的第3,4,5組中用分層抽樣的方法抽取6名學生進入第二輪面試,求第3,4,5組每組各抽取多少名學生進入第二輪面試?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京時間3月15日下午,谷歌圍棋人工智能![]() 與韓國棋手李世石進行最后一輪較量,
與韓國棋手李世石進行最后一輪較量,![]() 獲得本場比賽勝利,最終人機大戰總比分定格在
獲得本場比賽勝利,最終人機大戰總比分定格在![]() .人機大戰也引發全民對圍棋的關注,某學校社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查.根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖(如圖所示),將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.
.人機大戰也引發全民對圍棋的關注,某學校社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查.根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖(如圖所示),將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.
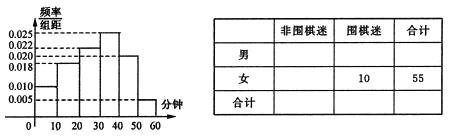
(1)根據已知條件完成如圖列聯表,并據此資料判斷你是否有![]() 的把握認為“圍棋迷”與性別有關?
的把握認為“圍棋迷”與性別有關?
(2)將上述調查所得到的頻率視為概率.現在從該地區大量學生中,采用隨機抽樣方法每次抽取1名學生,抽取3次,記所抽取的3名學生中的“圍棋迷”人數為![]() .若每次抽取的結果是相互獨立的,求
.若每次抽取的結果是相互獨立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.010 |
| 3.74 | 6.63 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com