對于數列an,(1)已知an是一個公差不為零的等差數列,a5=6.
①當a3=2時,若自然數n1,n2,…,nt,…滿足5<n1<n2<…<nt<…,且a3,a5,an1,an2,…,ant,…是等比數列,試用t表示nt;
②若存在自然數n1,n2,…,nt,…滿足5<n1<n2<…<nt<…,且a3,a5,an1,an2,…,ant,…構成一個等比數列.求證:當a3是整數時,a3必為12的正約數.
(2)若數列an滿足an+1an+3an+1+an+4=0,且a2009小于數列an中的其他任何一項,求a1的取值范圍.
【答案】
分析:(1)①在等差數列{a
n}中,由a
5=6,a
3=2,求出公差d,然后求出通項a
n,進而求出a
nt,由a
3,a
5a
n1,a
n2,…,a
nt…是等比數列,且可求出公比q,再求出a
nt,兩次求出的a
nt相等,找出n與t的關系;
②由a
3,a
5a
n1,a
n2,…,a
nt…是等比數列,由等比中項可得a
3a
n1=a
52,即
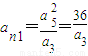
.,又由已知已知{a
n}是等差數列,可求
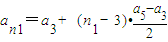
=
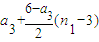
=
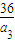
,整理可得

,由n為正整數可知a
3為12的正約數
(2)由a
n+1a
n+3a
n+1+a
n+4=0,得a
n+1a
n+2a
n+1+2a
n+4=a
n-a
n+1,
即(a
n+1+2)(a
n+2)=(a
n+2)-(a
n+1+2).a
2009小于數列a
n中的其他任何一項,可知a
n不是常數列,構造新的等差數列
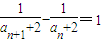
,并借助該數列的單調性與反證法求出a
1的范圍.
解答:解:(1)①因為a
3=2,a
5=6,所以,公差d=
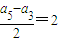
,
從而a
n=a
5+(n-5)d=2n-4(2分)
又a
3,a
5,a
n1,a
n2,a
nt,是等比數列,所以公比q=
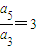
,所以
a
nt=a
5•3
t=2•3
t+1,t∈N
*.
又a
nt=2n
t-4,所以2n
t-4=2•3
t+1,所以
n
t=3
t+1+2,t∈N
*.(4分)
②因為n
1>5時,a
3,a
5,a
n1成等比數列,所以a
3a
n1=a
52,即
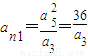
.(6分)
所以當n≥3時,
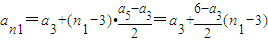
,
所以
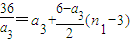
,
即
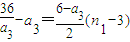
,
所以

.

,解得
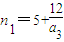
.
因為n
1是整數,且n
1>5,所以
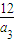
是正整數,從而整數a
3必為12的正約數.(8分)
(2)由a
n+1a
n+3a
n+1+a
n+4=0,得a
n+1a
n+2a
n+1+2a
n+4=a
n-a
n+1,
即(a
n+1+2)(a
n+2)=(a
n+2)-(a
n+1+2).(*)(10分)
由(*)知:若存在a
k=-2,則a
k+1=-2;若存在a
k+1=-2,則a
k=-2,所以a
n是常數列,與“a
2009小于數列a
n中的其他任何一項”矛盾,因此(a
n+1+2)(a
n+2)≠0.
由(*)式知
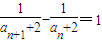
,從而數列
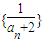
是首項為
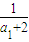
,公差為1的等差數列,即
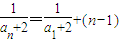
.(12分)
方法一由于數列
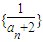
是遞增數列,且a
2009小于數列{a
n}中的其他任何一項,即a
2009+2小于數列{a
n+2}中的其他任何一項,所以a
2009+2<0,
且a
2010+2>0,這是因為若a
2009+2>0,則由
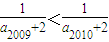
,
得a
2009+2>a
2010+2>0,即a
2009>a
2010,與
“a
2009小于數列a
n中的其他任何一項”矛盾:
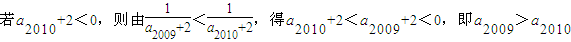
,與“a
2009小于數列a
n中的其他任何一項”矛盾:因此,
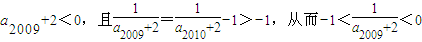
,
即

,
即
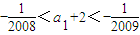
,
即-1

綜上,a
1的取值范圍是

方法二
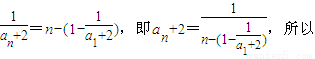
當n<1-
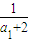
時,a
n+2單調遞增,且a
n+2<0;
當n>1-
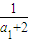
時,2+a
n單調遞減,且a
n+2>0.
由于a
2009小于數列{a
n}中的其他任何一項,即a
2009+2小于數列{a
n+2}中的其他任何一項,
所以a
2009+2<0,且a
2010+2>0,
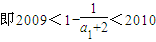
,
即-2009<
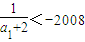
,
即-
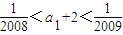
;
解得-
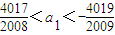
.
綜上,a
1的取值范圍是
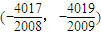
.(16分)
點評:本題是等差數列與等比數列的綜合應用,解答中要注意數列遞推公式與數列單調性的應用,屬于較難試題

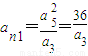 .,又由已知已知{an}是等差數列,可求
.,又由已知已知{an}是等差數列,可求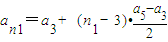 =
=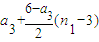 =
=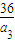 ,整理可得
,整理可得 ,由n為正整數可知a3為12的正約數
,由n為正整數可知a3為12的正約數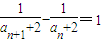 ,并借助該數列的單調性與反證法求出a1的范圍.
,并借助該數列的單調性與反證法求出a1的范圍.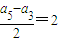 ,
,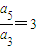 ,所以
,所以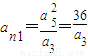 .(6分)
.(6分)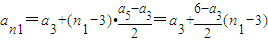 ,
,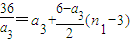 ,
,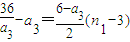 ,
, .
. ,解得
,解得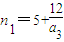 .
.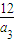 是正整數,從而整數a3必為12的正約數.(8分)
是正整數,從而整數a3必為12的正約數.(8分)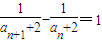 ,從而數列
,從而數列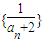 是首項為
是首項為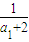 ,公差為1的等差數列,即
,公差為1的等差數列,即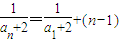 .(12分)
.(12分)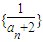 是遞增數列,且a2009小于數列{an}中的其他任何一項,即a2009+2小于數列{an+2}中的其他任何一項,所以a2009+2<0,
是遞增數列,且a2009小于數列{an}中的其他任何一項,即a2009+2小于數列{an+2}中的其他任何一項,所以a2009+2<0,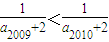 ,
,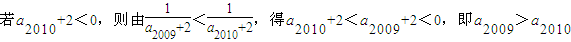 ,與“a2009小于數列an中的其他任何一項”矛盾:因此,
,與“a2009小于數列an中的其他任何一項”矛盾:因此,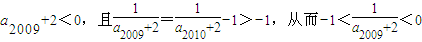 ,
, ,
,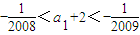 ,
,

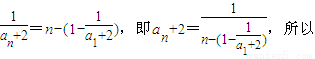
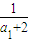 時,an+2單調遞增,且an+2<0;
時,an+2單調遞增,且an+2<0;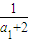 時,2+an單調遞減,且an+2>0.
時,2+an單調遞減,且an+2>0.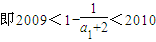 ,
,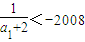 ,
,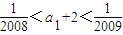 ;
;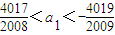 .
.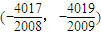 .(16分)
.(16分)

 備戰中考寒假系列答案
備戰中考寒假系列答案