
已知函數![]() ,在(-∞,-1),(2,+∞)上單調遞增,在(-1,2)上單調遞減,當且僅當x>4時,
,在(-∞,-1),(2,+∞)上單調遞增,在(-1,2)上單調遞減,當且僅當x>4時,![]() .
.
(Ⅰ)求函數f(x)的解析式;
(Ⅱ)若函數![]() 與函數f(x)、g(x)的圖象共有3個交點,求m的取值范圍.
與函數f(x)、g(x)的圖象共有3個交點,求m的取值范圍.
(I)f(x)= x3-![]() x2-6x-11
x2-6x-11
(II)m的取值范圍是(-21,-![]() )∪(1,5)∪(5,+∞)
)∪(1,5)∪(5,+∞)
(I)f(x)=3x2+2ax+b,由題意,-1,2是方程f’(x)=0的兩根.
∴ 4分
4分
∴f(x1)=x3-![]() x2-6x+0
x2-6x+0
令h(x)=f(x)-g(x)= x3-![]() x2-2x+c-5
x2-2x+c-5
h’(x)=3x2-5x-2=(3x+1) (x-2)
當x>4時,h’(x)>0,h(x)是增函數,∴h(4)=11+c=0 ∴c=-11 7分
∴f(x)= x3-![]() x2-6x-11 8分
x2-6x-11 8分
(Ⅱ)g(x)=(x-2)2+1 當x=2時,g(x)min=1
f(x)極大值=f(-1)=-![]() f(x)極小值=f(2)=-2l 11分
f(x)極小值=f(2)=-2l 11分
作出函數f(x)、g(x)的草圖,由圖可得,當函數y=m與函數f(x)、g(x)的圖象共有3個交點,
m的取值范圍是(-21,-![]() )∪(1,5)∪(5,+∞) 15分
)∪(1,5)∪(5,+∞) 15分


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
已知函數![]() 與
與![]() 在同一平面直角坐標系中的圖像如圖所示。記
在同一平面直角坐標系中的圖像如圖所示。記![]() 為“
為“![]() ”與“
”與“![]() ”時,
”時,![]() ,則下列關于函數
,則下列關于函數![]() 的說法中,正確的是
的說法中,正確的是
A.![]() B.
B.![]() 是函數
是函數![]() 的一個極小值
的一個極小值
C.方程![]() 有兩個實數根D.
有兩個實數根D.![]() 在(
在(![]() )上單調遞增
)上單調遞增
查看答案和解析>>
科目:高中數學 來源:2014屆遼寧朝陽高二下學期期中考試理科數學試卷(解析版) 題型:解答題
已知函數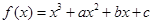 ,曲線
,曲線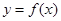 在點
在點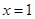 處的切線為
處的切線為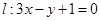 ,若
,若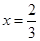 時,
時,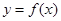 有極值.
有極值.
(1)求 的值;
的值;
(2)求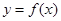 在
在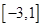 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源:2014屆吉林省高二上學期期中考試數學試卷(解析版) 題型:解答題
已知函數 定義在區間
定義在區間 上,
上, ,且當
,且當 時,
時,
恒有 .又數列
.又數列 滿足
滿足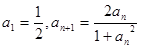 .
.
(1)證明: 在
在 上是奇函數;
上是奇函數;
(2)求 的表達式;
的表達式;
(3)設 為數列
為數列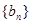 的前
的前 項和,若
項和,若 對
對 恒成立,求
恒成立,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2010年江蘇省高一第二次學情調研數學卷 題型:填空題
已知函數 和
和 在
在 的圖象如下圖表示:
的圖象如下圖表示:

給出下列四個命題:
①方程 有且僅有6個根; ②方程
有且僅有6個根; ②方程 有且僅有3個根;
有且僅有3個根;
③方程 有且僅有5個根; ④方程
有且僅有5個根; ④方程 有且僅有4個根;
有且僅有4個根;
其中正確命題的是_____★_____(注:把你認為是正確的序號都填上)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com