
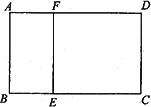
如圖,矩形ABCD中,AB=3,BC=4.E,F分別在線段BC和AD上,EF∥AB,將矩形ABEF沿EF折起,記折起后的矩形為MNEF,且平面MNEF⊥平面ECDF.
(Ⅰ)求證:NC∥平面MFD;
(Ⅱ)若EC=3,求證:ND⊥FC;
(Ⅲ)求四面體NFEC體積的最大值.
(1)證明:因為四邊形MNEF、EFDC都是矩形,
所以MN∥EF∥CD,MN=EF=CD
所以四邊形MNCD是平行四邊形,……………………2分
所以NC∥MD,……………………3分
因為NC![]() 平面MFD,MD
平面MFD,MD![]() 平面MFD,
平面MFD,
所以NC∥平面MFD……………………4分
(II)證明:連接ED,設ED![]() FC=O.
FC=O.
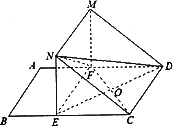
因為平面MNEF![]() 平面ECDF,且NE
平面ECDF,且NE![]() EF,
EF,
由面面垂直的性質定理得NE![]() 平面ECDF……………………5分
平面ECDF……………………5分
因為FC![]() 平面ECDF,所以FC
平面ECDF,所以FC![]() NE……………………6分
NE……………………6分
因為EC=CD,所以四邊形ECDF為正方形,所以FC![]() ED
ED
又ED![]() NE=E,所以FC
NE=E,所以FC![]() 平面NED……………………7分
平面NED……………………7分
因為ND![]() 平面NED,所以ND
平面NED,所以ND![]() FC……………………8分
FC……………………8分
(III)解:設NE=X,則EC=4-x,其中0<x<4
由(I)得NE![]() 平面FEC,
平面FEC,
所以四面體NFEC的體積為![]() ………………10分
………………10分
所以![]() ………………11分
………………11分
當且僅當x=4-x,即x=2時,四面體NFEC的體積最大.………………12分


科目:高中數學 來源: 題型:
 如圖,矩形ABCD中,AB=
如圖,矩形ABCD中,AB=8
| ||
| 3 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 A 若方程ax-x-a=0有兩個實數解,則a的取值范圍是
A 若方程ax-x-a=0有兩個實數解,則a的取值范圍是| AE |
| AF |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,矩形ABCD中,DC=
如圖,矩形ABCD中,DC=| 3 |
2
| ||||
| 12 |
2
| ||||
| 12 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (理)如圖,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如圖,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD| PQ |
| QD |
| BP |
| QD |
| ||
| 10 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com