
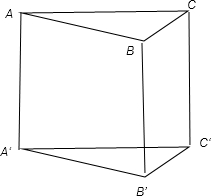
 解:根據題意,三棱柱的下底面的顏色互不相同,有A43=24種情況,
解:根據題意,三棱柱的下底面的顏色互不相同,有A43=24種情況,

 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
 (2012•杭州二模)已知正三棱柱ABC-A′B′C′的正視圖和側視圖如圖所示.設△ABC,△A′B′C′的中心分別是O,O′,現將此三棱柱繞直線OO′旋轉,在旋轉過程中對應的俯視圖的面積為S,則S的最大值為
(2012•杭州二模)已知正三棱柱ABC-A′B′C′的正視圖和側視圖如圖所示.設△ABC,△A′B′C′的中心分別是O,O′,現將此三棱柱繞直線OO′旋轉,在旋轉過程中對應的俯視圖的面積為S,則S的最大值為查看答案和解析>>
科目:高中數學 來源: 題型:
 已知正三棱柱ABC-A′B′C′的正視圖和側視圖如圖所示.設△ABC,△A′B′C′的中心分別是O、O′,現將此三棱柱繞直線OO′旋轉(包括逆時針方向和順時針方向),射線OA旋轉所成的角為x弧度(x可以取到任意一個實數),對應的俯視圖的面積記為S(x),則函數S(x)的最大值和最小正周期分別是( )
已知正三棱柱ABC-A′B′C′的正視圖和側視圖如圖所示.設△ABC,△A′B′C′的中心分別是O、O′,現將此三棱柱繞直線OO′旋轉(包括逆時針方向和順時針方向),射線OA旋轉所成的角為x弧度(x可以取到任意一個實數),對應的俯視圖的面積記為S(x),則函數S(x)的最大值和最小正周期分別是( )查看答案和解析>>
科目:高中數學 來源:2011年湖北省潛江中學高三數學滾動訓練20(理科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com