
【題目】給出下列四個說法,其中正確的是( )
A.命題“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
B.“![]() ”是“雙曲線
”是“雙曲線![]() 的離心率大于
的離心率大于![]() ”的充要條件
”的充要條件
C.命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命題“在![]() 中,若
中,若![]() ,則
,則![]() 是銳角三角形”的逆否命題是假命題
是銳角三角形”的逆否命題是假命題
【答案】D
【解析】
A選項:否命題應該對條件結論同時否定,說法不正確;
B選項:雙曲線![]() 的離心率大于
的離心率大于![]() ,解得
,解得![]() ,所以說法不正確;
,所以說法不正確;
C選項:否定應該是:![]() ,
,![]() ,所以說法不正確;
,所以說法不正確;
D選項:“在![]() 中,若
中,若![]() ,則
,則![]() 是銳角三角形”是假命題,所以其逆否命題也為假命題,所以說法正確.
是銳角三角形”是假命題,所以其逆否命題也為假命題,所以說法正確.
命題“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”,所以A選項不正確;
”,所以A選項不正確;
雙曲線![]() 的離心率大于
的離心率大于![]() ,即
,即![]() ,解得
,解得![]() ,則“
,則“![]() ”是“雙曲線
”是“雙曲線![]() 的離心率大于
的離心率大于![]() ”的充分不必要條件,所以B選項不正確;
”的充分不必要條件,所以B選項不正確;
命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”, 所以C選項不正確;
”, 所以C選項不正確;
命題“在![]() 中,若
中,若![]() ,則
,則![]() 是銳角三角形”, 在
是銳角三角形”, 在![]() 中,若
中,若![]() ,可能
,可能![]() ,此時三角形不是銳角三角形,所以這是一個假命題,所以其逆否命題也是假命題,所以該選項說法正確.
,此時三角形不是銳角三角形,所以這是一個假命題,所以其逆否命題也是假命題,所以該選項說法正確.
故選:D


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,E為PD的中點.

(1) 證明:PB∥平面AEC
(2) 設二面角D-AE-C為60°,AP=1,AD=![]() ,求三棱錐E-ACD的體積
,求三棱錐E-ACD的體積
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 中,邊
中,邊![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,![]() ,過
,過![]() 邊上一點
邊上一點![]() (異于端點)引邊
(異于端點)引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,再由
,再由![]() 引邊
引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,又由
,又由![]() 引邊
引邊![]() 的垂線
的垂線![]() ,垂足為
,垂足為![]() ,同樣的操作連續進行,得到點列
,同樣的操作連續進行,得到點列![]() 、
、![]() 、
、![]() ,設
,設![]() (
(![]() );
);
(1)求![]() ;
;
(2)結論“![]() ”是否正確?請說明理由;
”是否正確?請說明理由;
(3)若對于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2018年10月考考試中,成都外國語學校共有250名高三文科學生參加考試,數學成績的頻率分布直方圖如圖:
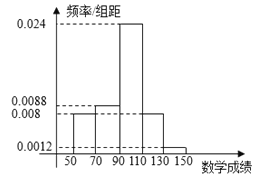
(1)如果成績大于130的為特別優秀,這250名學生中本次考試數學成績特別優秀的大約多少人?
(2)如果這次考試語文特別優秀的有5人,語文和數學兩科都特別優秀的共有2人,從(1)中的數學成績特別優秀的人中隨機抽取2人,求選出的2人中恰有1名兩科都特別優秀的概率.
(3)根據(1),(2)的數據,是否有99%以上的把握認為語文特別優秀的同學,數學也特別優秀?
①![]()
②
P( | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某部門經統計,客戶對不同款型理財產品的最滿意程度百分比和對應的理財總銷售量(萬元)如下表(最滿意度百分比超高時總銷售量最高):
產品款型 | A | B | C | D | E | F | G | H | I | J |
最滿意度% | 20 | 34 | 25 | 19 | 26 | 20 | 19 | 24 | 19 | 13 |
總銷量(萬元) | 80 | 89 | 89 | 78 | 75 | 71 | 65 | 62 | 60 | 52 |
設![]() 表示理財產品最滿意度的百分比,
表示理財產品最滿意度的百分比,![]() 為該理財產品的總銷售量(萬元).這些數據的散點圖如圖所示.
為該理財產品的總銷售量(萬元).這些數據的散點圖如圖所示.
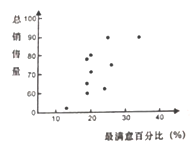
(1)在![]() 份
份![]() 款型理財產品的顧客滿意度調查資料中任取
款型理財產品的顧客滿意度調查資料中任取![]() 份;只有一份最滿意的,求含有最滿意客戶資料事件的概率.
份;只有一份最滿意的,求含有最滿意客戶資料事件的概率.
(2)我們約定:相關系數的絕對值在![]() 以下是無線性相關,在
以下是無線性相關,在![]() 以上(含
以上(含![]() )至
)至![]() 是一般線性相關,在
是一般線性相關,在![]() 以上(含
以上(含![]() )是較強線性相關,若沒有達到較強線性相關則采取“末位”剔除制度(即總銷售量最少的那一款產品退出理財銷售);試求在剔除“末位”款型后的線性回歸方程(系數精確到
)是較強線性相關,若沒有達到較強線性相關則采取“末位”剔除制度(即總銷售量最少的那一款產品退出理財銷售);試求在剔除“末位”款型后的線性回歸方程(系數精確到![]() ).
).
數據參考計算值:
項目 |
|
|
|
|
|
|
值 | 21.9 | 72.1 | 288.9 | 37.16 | 452.1 | 17.00 |
附:回歸直線方程![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為:
線性相關系數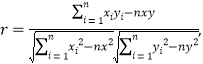
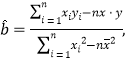
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某幼兒園舉辦“yue”主題系列活動——“悅”動越健康親子運動打卡活動,為了解小朋友堅持打卡的情況,對該幼兒園所有小朋友進行了調查,調查結果如下表:
打卡天數 | 17 | 18 | 19 | 20 | 21 |
男生人數 | 3 | 5 | 3 | 7 | 2 |
女生人數 | 3 | 5 | 5 | 7 | 3 |
(1)根據上表數據,求該幼兒園男生平均打卡的天數;
(2)若從打卡21天的小朋友中任選2人交流心得,求選到男生和女生各1人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的焦距為
的焦距為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 為坐標原點).
為坐標原點).
(1)求橢圓![]() 的標準方程.
的標準方程.
(2)已知動直線![]() 與圓
與圓![]() :
:![]() 相切,且與橢圓
相切,且與橢圓![]() 交于
交于![]() ,
,![]() 兩點.是否存在實數
兩點.是否存在實數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com