
已知a、b是兩個非零向量,同時滿足|a|=|b|=|a-b|,求a與a+b的夾角.
|
解法 1:根據|a|=|b|,有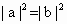 . .
又由 |b|=|a-b|,得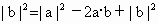 . .
∴ 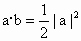 . .
而 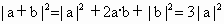 . .
∴ 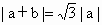 . .
設 a與a+b的夾解為q ,則
∴q =30°. 解法2:設向量 ∵|a|=|b|,∴ 由|b|=|a-b|,得 由 得 設a與a+b的夾解為q ,則
∴q =30°. 解法3:根據向量加法的幾何意義,作圖如圖.
在平面內任取一點 O,作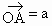 , ,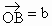 ,以 ,以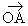 、 、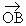 為鄰邊作平行四邊行OACB. 為鄰邊作平行四邊行OACB.
∵ |a|=|b|,即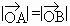 , ,
∴平行四邊行 OACB為菱形,OC平分∠AOB.這時 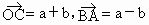 . .
而 |a|=|b|=|a-b|,即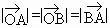 . .
∴△ AOB為三角形,則∠AOB=60°.于是∠ AOC=30°,即a與a+b的夾角為30°. |
|
基于平面向量的表示上的差異,也就是表示方法的不同,才產生了以上三種不同的解法,對于本題的三種解法同學們都要認真理解. |


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分條件 |
| B、必要條件 |
| C、充要條件 |
| D、既不充分也不必要條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com