Question

已知函數f（x）=2ax³-3ax²+1，g(x)=-

a

4

x+

3

2

．（a∈R）
（I）當a=1時，求函數y=f（x）的單調區間；
（II）若任意給定的x₀∈[0，2]，在[0，2]上總存在兩個不同的x_i（i=1，2），使得f（x_i）=g（x₀）成立，求a的取值范圍．

Answer 1

分析：（I）由題意先把a代入使得函數f（x）具體，再利用導函數求其單調區間；
（II）由題意可以把問題轉化為求函數f（x）和函數g（x）的值域，并有題意轉化為兩個函數的值域的關系問題．

解答：解：（I）f'（x）=6x²-6x=6x（x-1）．
由f'（x）＞0，得x＞1或x＜0；
由f'（x）＜0，得0＜x＜1；
故函數f（x）的單調遞增區間是（-∞，0]，[1，+∞）；
單調遞減區間是[0，1]．
（II）f^′（x）=6ax²-6ax=6ax（x-1）．
①當a=0時，顯然不可能；
②當a＞0時，函數f（x）的變化情況如下表所示

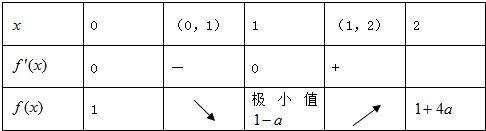
又因為當a＞0時，g(x)=-

a

4

x+

3

2

在[0，2]上是減函數，
對任意x∈[0，2]，g(x)∈[-

a

2

+

3

2

，

3

2

]，不合題意；
③當a＜0時，函數f（x）的變化情況如下表所示


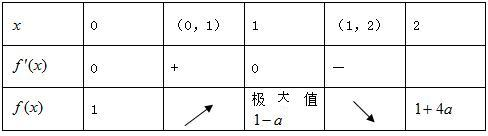
又因為當a＜0時，g(x)=-

a

4

x+

3

2

在[0，2]上是增函數，
對任意x∈[0，2]，g(x)∈[

3

2

，-

a

2

+

3

2

]，
由題意可得，-

a

2

+

3

2

＜1-a
∴a＜-1
綜上，a的取值范圍為（-∞，-1）．

點評：（I）在此重點考查了利用函數的導函數求其單調區間并且還考查了一元二次方程的求解方法；
（II）在此主要考查了等價轉化的思想，還有利用導函數求函數的最值并考查了含有字母時分類討論的思想，及集合之間的關系．