
【題目】已知函數(shù)![]() .
.
(I)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)若![]() 在
在![]() 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(III)在(II)的條件下,對任意的![]() ,求證:
,求證:![]() .
.
【答案】(I)當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,無單調(diào)遞減區(qū)間,當(dāng)
上單調(diào)遞增,無單調(diào)遞減區(qū)間,當(dāng)![]() 時,
時,![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,單調(diào)遞減區(qū)間為
,單調(diào)遞減區(qū)間為![]() ;(II)
;(II)![]() ;(III)證明見解析.
;(III)證明見解析.
【解析】試題分析:(I)利用![]() 時
時![]() 為單調(diào)增函數(shù),
為單調(diào)增函數(shù),![]() 時
時![]() 為單調(diào)減函數(shù)這一性質(zhì)來分情況討論題中
為單調(diào)減函數(shù)這一性質(zhì)來分情況討論題中![]() 單調(diào)區(qū)間問題;(II)根據(jù)函數(shù)單調(diào)性與最值,若
單調(diào)區(qū)間問題;(II)根據(jù)函數(shù)單調(diào)性與最值,若![]() 在
在![]() 上恒成立,則函數(shù)的最大值小于或等于零.當(dāng)
上恒成立,則函數(shù)的最大值小于或等于零.當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() ,說明
,說明![]() 時
時![]() ,不合題意舍去.當(dāng)
,不合題意舍去.當(dāng)![]() 時,
時,![]() 的最大值小于零.但
的最大值小于零.但![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 只能等于零.令
只能等于零.令![]() 即可求得答案;(III)首先將
即可求得答案;(III)首先將![]() 的表達(dá)式表達(dá)出來,化簡轉(zhuǎn)化為
的表達(dá)式表達(dá)出來,化簡轉(zhuǎn)化為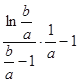 的形式,再根據(jù)(II)的結(jié)論得到
的形式,再根據(jù)(II)的結(jié)論得到![]() ,后逐步化簡
,后逐步化簡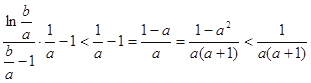 ,原命題得證.
,原命題得證.
試題解析:(I)![]() ,
,
當(dāng)![]() 時,
時,![]() 恒成立,則函數(shù)
恒成立,則函數(shù)![]() 在
在![]() 上單調(diào)遞增,無單調(diào)遞減區(qū)間;
上單調(diào)遞增,無單調(diào)遞減區(qū)間;
當(dāng)![]() 時,由
時,由![]() ,得
,得![]() ,由
,由![]() ,
,
得![]() ,此時
,此時![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,單調(diào)遞減區(qū)間為
,單調(diào)遞減區(qū)間為![]() .
.
(II)由(I)知:當(dāng)![]() 時,
時,![]() 在
在![]() 上遞增,
上遞增,![]() ,顯然不成立;
,顯然不成立;
當(dāng)![]() 時,
時,![]() ,只需
,只需![]() 即可,
即可,
令![]() ,則
,則![]() ,
,![]()
![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
![]() .
.
![]() 對
對![]() 恒成立,也就是
恒成立,也就是![]() 對
對![]() 恒成立,
恒成立,
![]() ,解得
,解得![]() ,
,![]() 若
若![]() 在
在![]() 上恒成立,則
上恒成立,則![]() .
.
(III)證明: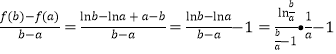 ,
,
由(II)得![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 時取等號,
時取等號,
又由![]() 得
得![]() ,所以有
,所以有![]() ,即
,即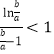 .
.
則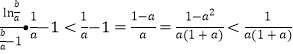 ,
,
則原不等式![]() 成立. ………(12分)
成立. ………(12分)



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱錐P—ABC中,PC![]() 底面ABC,AB=BC,D、F分別為AC、PC的中點(diǎn),DE
底面ABC,AB=BC,D、F分別為AC、PC的中點(diǎn),DE![]() AP于E。(1)求證:AP
AP于E。(1)求證:AP![]() 平面BDE;(2)求證:平面BDE
平面BDE;(2)求證:平面BDE![]() 平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱錐P—ABC所成上、下兩部分的體積比。
平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱錐P—ABC所成上、下兩部分的體積比。

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)求與圓心在直線![]() 上,且過點(diǎn)A(2,-3),B(-2,-5)的圓C的方程.
上,且過點(diǎn)A(2,-3),B(-2,-5)的圓C的方程.
(2)設(shè)![]() 是圓C上的點(diǎn),求
是圓C上的點(diǎn),求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)已知函數(shù)f(x)(x∈R)是奇函數(shù),且當(dāng)x>0時,f(x)=2x-1,求函數(shù)f(x)的解析式.
(2)已知x+y=12,xy=9且x<y,求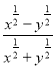 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為棱
為棱![]() 的中點(diǎn).
的中點(diǎn).
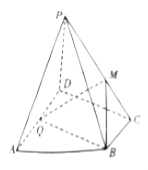
(I)證明:![]() 平面
平面![]() ;
;
(II)已知![]() ,求
,求![]() 點(diǎn)到平面
點(diǎn)到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某車間20名工人年齡數(shù)據(jù)如下表:
年齡(歲) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合計(jì) |
工人數(shù)(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求這20名工人年齡的眾數(shù)與平均數(shù);
(2)以十位數(shù)為莖,個位數(shù)為葉,作出這20名工人年齡的莖葉圖;
(3)從年齡在24和26的工人中隨機(jī)抽取2人,求這2人均是24歲的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高三一次月考之后,為了為解數(shù)學(xué)學(xué)科的學(xué)習(xí)情況,現(xiàn)從中隨機(jī)抽出若干名學(xué)生此次的數(shù)學(xué)成績,按成績分組,制成了下面頻率分布表:
組號 | 分組 | 頻數(shù) | 頻率 |
第一組 |
| 5 | 0.05 |
第二組 |
| 35 | 0.35 |
第三組 |
| 30 | 0.30 |
第四組 |
| 20 | 0.20 |
第五組 |
| 10 | 0.10 |
合計(jì) | 100 | 1.00 | |
(1)試估計(jì)該校高三學(xué)生本次月考的平均分;
(2)如果把表中的頻率近似地看作每個學(xué)生在這次考試中取得相應(yīng)成績的概率,那么從所有學(xué)生中采用逐個抽取的方法任意抽取3名學(xué)生的成績,并記成績落在![]() 中的學(xué)生數(shù)為
中的學(xué)生數(shù)為![]() ,
,
求:①在三次抽取過程中至少有兩次連續(xù)抽中成績在![]() 中的概率;
中的概率;
②![]() 的分布列和數(shù)學(xué)期望.(注:本小題結(jié)果用分?jǐn)?shù)表示)
的分布列和數(shù)學(xué)期望.(注:本小題結(jié)果用分?jǐn)?shù)表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合P={x|a+1≤x≤2a+1},Q={x|1≤2x+5≤15}.
(1)已知a=3,求(RP)∩Q;
(2)若P∪Q=Q,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合A={x|ax2-3x+2=0}.
(1)若A是單元素集合,求集合A;
(2)若A中至少有一個元素,求a的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com