
【題目】如圖,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
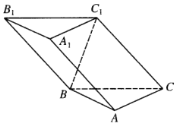
(Ⅰ)證明:點![]() 在底面
在底面![]() 上的射影
上的射影![]() 必在直線
必在直線![]() 上;
上;
(Ⅱ)若二面角![]() 的大小為
的大小為![]() ,
,![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)見解析(Ⅱ)![]()
【解析】
(Ⅰ)利用面面垂直的判定定理與性質(zhì)定理證明;
(Ⅱ)以![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標(biāo)系.利用向量法求解可得結(jié)果.
軸建立空間直角坐標(biāo)系.利用向量法求解可得結(jié)果.
(Ⅰ)證明:連接![]() ,如圖:
,如圖:

因為![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]()
所以平面![]() 平面
平面![]() .
.
過點![]() 作
作![]() ,
,
則由面面垂直的性質(zhì)定理可知![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 與
與![]() 重合,
重合,
所以點![]() 在底面
在底面![]() 上的射影
上的射影![]() 必在直線
必在直線![]() 上.
上.
(Ⅱ)由![]() ,
,![]() ,得
,得![]() 是二面角
是二面角![]() 的平面角,即
的平面角,即![]() .
.
在平面![]() 內(nèi),過點
內(nèi),過點![]() 作
作![]() ,以
,以![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸建立如圖所示的空間直角坐標(biāo)系.
軸建立如圖所示的空間直角坐標(biāo)系.

在![]() 中,由
中,由![]() ,
,![]() ,得
,得![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() 是邊長為2的等邊三角形,
是邊長為2的等邊三角形,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
由![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
則 ,即
,即 ,所以
,所以![]() ,
,
取![]() ,則
,則![]()
所以平面![]() 的一個法向量為
的一個法向量為![]() .
.
設(shè)![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
故 .
.


 巧學(xué)巧練系列答案
巧學(xué)巧練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 是
是![]() 上的奇函數(shù),其中
上的奇函數(shù),其中![]() ,則下 列關(guān)于函數(shù)
,則下 列關(guān)于函數(shù)![]() 的描述中,其中正確的是( )
的描述中,其中正確的是( )
①將函數(shù)![]() 的圖象向右平移
的圖象向右平移![]() 個單位可以得到函數(shù)
個單位可以得到函數(shù)![]() 的圖象;
的圖象;
②函數(shù)![]() 圖象的一條對稱軸方程為
圖象的一條對稱軸方程為![]() ;
;
③當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 的最小值為
的最小值為![]() ;
;
④函數(shù)![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
A.①③B.③④C.②③D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,準(zhǔn)線
,準(zhǔn)線![]() 與
與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 的直線交拋物線于
的直線交拋物線于![]() ,
,![]() 兩點,點
兩點,點![]() 在第一象限.
在第一象限.
![]() 若
若![]() ,
,![]() ,求直線
,求直線![]() 的方程;
的方程;
![]() 若
若![]() ,點
,點![]() 為準(zhǔn)線
為準(zhǔn)線![]() 上任意一點,求證:直線
上任意一點,求證:直線![]() ,
,![]() ,
,![]() 的斜率成等差數(shù)列.
的斜率成等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某生物研究所為研發(fā)一種新疫苗,在200只小白鼠身上進(jìn)行科研對比實驗,得到如下統(tǒng)計數(shù)據(jù):
未感染病毒 | 感染病毒 | 總計 | |
未注射疫苗 | 30 |
|
|
注射疫苗 | 70 |
|
|
總計 | 100 | 100 | 200 |
現(xiàn)從未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率為![]() .
.
(Ⅰ)能否有![]() 的把握認(rèn)為注射此種疫苗有效?
的把握認(rèn)為注射此種疫苗有效?
(Ⅱ)在未注射疫苗且未感染病毒與注射疫苗且感染病毒的小白鼠中,分別抽取3只進(jìn)行病例分析,然后從這6只小白鼠中隨機抽取2只對注射疫苗情況進(jìn)行核實,求抽到的2只均是注射疫苗且感染病毒的小白鼠的概率.
附: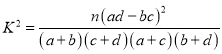 ,
,![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求證:數(shù)列![]() 為等比數(shù)列;
為等比數(shù)列;
(2)設(shè)數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() 為定值;
為定值;
(3)判斷數(shù)列![]() 中是否存在三項成等差數(shù)列,并證明你的結(jié)論.
中是否存在三項成等差數(shù)列,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在黨中央的正確領(lǐng)導(dǎo)下,通過全國人民的齊心協(xié)力,特別是全體一線醫(yī)護(hù)人員的共同努力,新冠肺炎疫情得到了有效控制.作為集中醫(yī)學(xué)觀察隔離點的某酒店在疫情期間,為客人提供兩種速食品—“方便面”和“自熱米飯”.為調(diào)查這兩種速食品的受歡迎程度,酒店部門經(jīng)理記錄了連續(xù)10天這兩種速食品的銷售量,得到如下頻數(shù)分布表(其中銷售量單位:盒):
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方便面 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 |
自熱米飯 | 88 | 96 | 98 | 97 | 101 | 99 | 102 | 107 | 104 | 112 |
(1)根據(jù)兩組數(shù)據(jù)完成下面的莖葉圖(填到答題卡上);

(2)根據(jù)統(tǒng)計學(xué)知識,你認(rèn)為哪種速食品更受歡迎,并簡要說明理由;
(3)求自熱米飯銷售量y關(guān)于天數(shù)t的線性回歸方程,并預(yù)估第12天自熱米飯的銷售量(結(jié)果精確到整數(shù)).
參考數(shù)據(jù):![]() ,
,![]() .
.
附:回歸直線方程![]() ,其中
,其中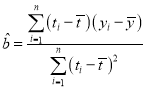 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種治療新型冠狀病毒感染肺炎的復(fù)方中藥產(chǎn)品的質(zhì)量以其質(zhì)量指標(biāo)值衡量,質(zhì)量指標(biāo)越大表明質(zhì)量越好,為了提高產(chǎn)品質(zhì)量,我國醫(yī)療科研專家攻堅克難,新研發(fā)出![]() 、
、![]() 兩種新配方,在兩種新配方生產(chǎn)的產(chǎn)品中隨機抽取數(shù)量相同的樣本,測量這些產(chǎn)品的質(zhì)量指標(biāo)值,規(guī)定指標(biāo)值小于
兩種新配方,在兩種新配方生產(chǎn)的產(chǎn)品中隨機抽取數(shù)量相同的樣本,測量這些產(chǎn)品的質(zhì)量指標(biāo)值,規(guī)定指標(biāo)值小于![]() 時為廢品,指標(biāo)值在
時為廢品,指標(biāo)值在![]() 為一等品,大于
為一等品,大于![]() 為特等品.現(xiàn)把測量數(shù)據(jù)整理如下,其中
為特等品.現(xiàn)把測量數(shù)據(jù)整理如下,其中![]() 配方廢品有
配方廢品有![]() 件.
件.
![]() 配方的頻數(shù)分布表
配方的頻數(shù)分布表
質(zhì)量指標(biāo)值分組 |
|
|
|
|
|
頻數(shù) |
|
|
|
|
|

(1)求![]() ,
,![]() 的值;
的值;
(2)試確定![]() 配方和
配方和![]() 配方哪一種好?(說明:在統(tǒng)計方法中,同一組數(shù)據(jù)常用該組區(qū)間的中點值作為代表)
配方哪一種好?(說明:在統(tǒng)計方法中,同一組數(shù)據(jù)常用該組區(qū)間的中點值作為代表)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某植物園內(nèi)有一塊圓形區(qū)域,在其內(nèi)接四邊形![]() 內(nèi)種植了兩種花卉,其中
內(nèi)種植了兩種花卉,其中![]() 區(qū)域內(nèi)種植蘭花,
區(qū)域內(nèi)種植蘭花,![]() 區(qū)域內(nèi)種植丁香花,對角線BD是一條觀賞小道.測量可知邊界
區(qū)域內(nèi)種植丁香花,對角線BD是一條觀賞小道.測量可知邊界![]() ,
,![]() ,
, ![]() .
.
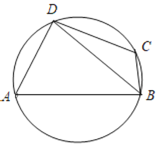
(1)求觀賞小道BD的長及種植區(qū)域![]() 的面積;
的面積;
(2)因地理條件限制,種植丁香花的邊界BC,CD不能變更,而邊界AB,AD可以調(diào)整,使得種植蘭花的面積有所增加,請在BAD上設(shè)計一點P,使得種植區(qū)域改造后的新區(qū)域(四邊形![]() )的面積最大,并求出這個面積的最大值.
)的面積最大,并求出這個面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在長方體ABCD﹣HKLE中,底面ABCD是邊長為3的正方形,對角線AC與BD相交于點O,點F在線段AH上,且![]() ,BE與底面ABCD所成角為
,BE與底面ABCD所成角為![]() .
.
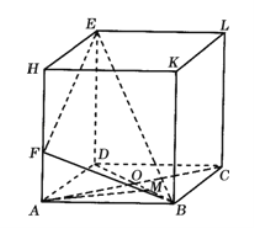
(1)求證:AC⊥BE;
(2)求二面角F﹣BE﹣D的余弦值;
(3)設(shè)點M在線段BD上,且AM//平面BEF,求DM的長.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com