
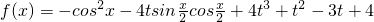 ,x∈R,
,x∈R,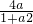 成立?如果存在,求出這樣的a及其對應的t;如果不存在,請說明理由.
成立?如果存在,求出這樣的a及其對應的t;如果不存在,請說明理由.解:(1)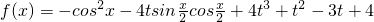 =sin2x-1-2tsinx+4t3+t2-3t+4=sin2x-2tsinx+t2+4t3-3t+3=(sinx-t)2+4t3-3t+3.
=sin2x-1-2tsinx+4t3+t2-3t+4=sin2x-2tsinx+t2+4t3-3t+3=(sinx-t)2+4t3-3t+3.
由(sinx-t)2≥0,|t|≤1,故當sinx=t時,f(x)有最小值g(t),即
g(t)=4t3-3t+3.
(2)我們有g'(t)=12t2-3=3(2t+1)(2t-1),-1<t<1.
列表如下:
| t | (-1,- ) ) | - | (- , , ) ) |  | ( ,1) ,1) |
| g'(t) | + | 0 | - | 0 | + |
| G(t) | ↗ | 極大值g(- ) ) | ↘ | 極小值g( ) ) | ↗ |
由此可見,g(t)在區間(-1,- )和(
)和( ,1)單調增加,在區間(-
,1)單調增加,在區間(- ,
, )單調減小,極小值為g(
)單調減小,極小值為g( )=2,
)=2,
又g(-1)=-4-(-3)+3=2
故g(t)在[-1,1]上的最小值為2
注意到:對任意的實數a,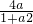 =
=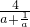 ∈[-2,2]
∈[-2,2]
當且僅當a=1時,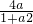 =2,對應的t=-1或
=2,對應的t=-1或 ,
,
故當t=-1或 時,這樣的a存在,且a=1,使得g(t)≥
時,這樣的a存在,且a=1,使得g(t)≥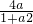 成立.
成立.
而當t∈(-1,1]且t≠ 時,這樣的a不存在.
時,這樣的a不存在.
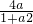 成立,即
成立,即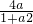 ≥g(t)的最大值,求出a的范圍.
≥g(t)的最大值,求出a的范圍.

 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源:南京師范大學附屬揚子中學2008屆高三年級數學課堂限時訓練(三角函數和向量部分六) 題型:044
設函數
(1)求g(t)的表達式;
(2)討論g(t)在區間(-1,1)內的單調性并求極值
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
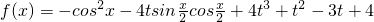 ,x∈R,其中|t|≤1,將f(x)的最小值記為g(t).
,x∈R,其中|t|≤1,將f(x)的最小值記為g(t).查看答案和解析>>
科目:高中數學 來源:2012-2013學年寧夏銀川一中高三(下)第六次月考數學試卷(文科)(解析版) 題型:解答題
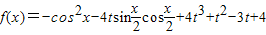 ,x∈R,其中|t|≤1,將f(x)的最小值記為g(t).
,x∈R,其中|t|≤1,將f(x)的最小值記為g(t).查看答案和解析>>
科目:高中數學 來源:2010年安徽省淮南二中高三(上)第二次月考數學試卷(文科)(解析版) 題型:解答題
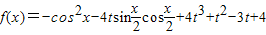 ,x∈R,
,x∈R,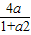 成立?如果存在,求出這樣的a及其對應的t;如果不存在,請說明理由.
成立?如果存在,求出這樣的a及其對應的t;如果不存在,請說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com