已知函數(shù)

(1)求函數(shù)

的最小值及單調(diào)減區(qū)間;
(2)在


中,

分別是角

的對邊,且

,

,

,且

,求

,c的值
(1)最小值為-1,單調(diào)減區(qū)間為
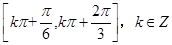
;(2)
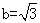
,
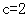
試題分析:(1)因為已知函數(shù)

通過化一公式函數(shù)
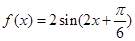
.又因為函數(shù)
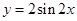
的單調(diào)遞減區(qū)間是
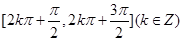
.所以可得
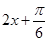
在該區(qū)間內(nèi)的范圍即可求得
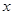
的范圍.
(2)因為在


中,

分別是角

的對邊,且

由(1)式可求得角A的值.再利用余弦定理即可得可求得三角形中的邊
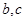
的關系.從而即可求出
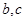
的值.
試題解析:(1)

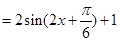
∴函數(shù)

的最小值為
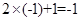
由
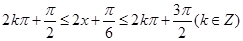
得:
單調(diào)減區(qū)間為
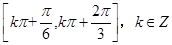
6分
(2)
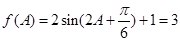
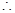
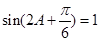
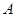
是三角形內(nèi)角,∴
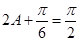
即
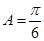
∴
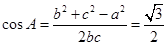
即:
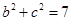
.
將

代入可得:
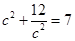
,解之得:
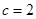
或
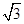
.
∴,
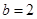
或
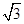
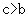
, ∴
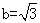
,
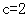
, 13分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
設△
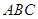
的內(nèi)角
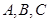
所對邊的長分別為
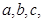
,且有
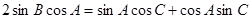
.
(Ⅰ)求角A的大小;
(Ⅱ)若
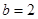
,
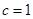
,
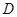
為
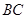
的中點,求
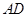
的長.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知
a,
b,
c分別為△
ABC的三個內(nèi)角
A,
B,
C的對邊,向量
m=(

,-1),
n=(cos
A,sin
A).若
m⊥
n,且
acos
C+
ccos
A=
bsin
B,則角
C的大小為________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖,在△
ABC中,
AB=
AC=2,
BC=2

,點
D在
BC邊上,∠
ADC=75°,則
AD的長為________.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在

中,記角

、

、

所對的邊分別為

、

、

,且這三角形的三邊長是公差為1的等差數(shù)列,若最小邊

,則

( ).
查看答案和解析>>


 的最小值及單調(diào)減區(qū)間;
的最小值及單調(diào)減區(qū)間;
 中,
中, 分別是角
分別是角 的對邊,且
的對邊,且 ,
, ,
, ,且
,且 ,求
,求 ,c的值
,c的值 ,-1),n=(cos A,sin A).若m⊥n,且acos C+ccos A=bsin B,則角C的大小為________.
,-1),n=(cos A,sin A).若m⊥n,且acos C+ccos A=bsin B,則角C的大小為________.