
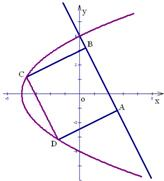
 矩形ABCD的頂點A、B在直線l:2x+y-4=0上運動,點C,D曲線E:y2=4(x+4)(-4≤x≤4)上運動,求矩形ABCD面積的最大值.
矩形ABCD的頂點A、B在直線l:2x+y-4=0上運動,點C,D曲線E:y2=4(x+4)(-4≤x≤4)上運動,求矩形ABCD面積的最大值.| 2 |
| 2 |
| 17 |
| 2 |
| |4-b| | ||
|
| 2b+17 |
| 17 |
| 2 |
| 2 |
| 2b+17 |
| 17 |
| 2 |
| 2 |
|
|
|
| 2 |
| 2 |
| 17 |
| 2 |
| b2-16 |
| 4 |
| 5[(x1+x2)2-4x1x2] |
| 5(2b+17) |
| |4-b| | ||
|
| 2b+17 |
| 17 |
| 2 |
| 2 |
| 17 |
| 2 |
| 13 |
| 3 |
| 17 |
| 2 |
| 13 |
| 3 |
| 13 |
| 3 |
| 2 |
| 13 |
| 3 |
| 2 |
| 13 |
| 3 |
125
| ||
| 9 |
|
|
|
| 2 |
| 2 |
| 17 |
| 2 |
| b2-16 |
| 4 |
| 5[(x1+x2)2-4x1x2] |
| 5(2b+17) |
| |4-b| | ||
|
| 2b+17 |
| 17 |
| 2 |
| 2 |
| 2b+17 |
| 2b+17 |
| 4-b |
| 4-b |
(
|
(
|
125
| ||
| 9 |
| 13 |
| 3 |


科目:高中數學 來源: 題型:
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
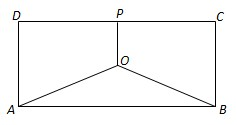 某地有三家工廠,分別位于矩形ABCD的頂點A、B及CD的中點P處,已知AB=20km,BC=10km,為了處理三家工廠的污水,現要在矩形ABCD的區域上(含邊界),且A、B與等距離的一點O處建造一個污水處理廠,并鋪設排污管道AO、BO、OP,設排污管道的總長為ykm.
某地有三家工廠,分別位于矩形ABCD的頂點A、B及CD的中點P處,已知AB=20km,BC=10km,為了處理三家工廠的污水,現要在矩形ABCD的區域上(含邊界),且A、B與等距離的一點O處建造一個污水處理廠,并鋪設排污管道AO、BO、OP,設排污管道的總長為ykm.查看答案和解析>>
科目:高中數學 來源: 題型:
(08年江蘇卷)某地有三家工廠,分別位于矩形ABCD的頂點A,B,及CD的中點P處,已知![]() km,
km, ![]() ,為了處理三家工廠的污水,現要在矩形ABCD的區域上(含邊界),且A,B與等距離的一點O處建造一個污水處理廠,并鋪設排污管道AO,BO,OP,設排污管道的總長為ykm。
,為了處理三家工廠的污水,現要在矩形ABCD的區域上(含邊界),且A,B與等距離的一點O處建造一個污水處理廠,并鋪設排污管道AO,BO,OP,設排污管道的總長為ykm。
 (I)按下列要求寫出函數關系式:
(I)按下列要求寫出函數關系式:
① 設![]() ,將
,將![]() 表示成
表示成![]() 的函數關系式;
的函數關系式;
② 設![]() ,將
,將![]() 表示成
表示成![]() 的函數關系式。
的函數關系式。
(II)請你選用(I)中的一個函數關系式,確定污水處理廠的位置,使三條排水管道總長度最短。
查看答案和解析>>
科目:高中數學 來源:2008年普通高等學校招生全國統一考試數學試題(江蘇卷) 題型:解答題
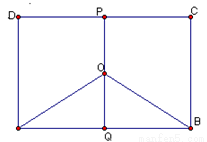
某地有三家工廠,分別位于矩形ABCD的頂點A,B,及CD的中點P處,已知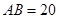 km,
km, 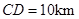 ,為了處理三家工廠的污水,現要在矩形ABCD的區域上(含邊界),且A,B與等距離的一點O處建造一個污水處理廠,并鋪設排污管道AO,BO,OP,設排污管道的總長為ykm。
,為了處理三家工廠的污水,現要在矩形ABCD的區域上(含邊界),且A,B與等距離的一點O處建造一個污水處理廠,并鋪設排污管道AO,BO,OP,設排污管道的總長為ykm。
(I)按下列要求寫出函數關系式:
①設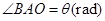 ,將
,將 表示成
表示成 的函數關系式;
的函數關系式;
②設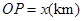 ,將
,將 表示成
表示成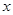 的函數關系式。
的函數關系式。
(Ⅱ)請你選用(I)中的一個函數關系式,確定污水處理廠的位置,使三條排水管道總長度最短。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com