
(本小題14分)如圖,在平面直角坐標(biāo)系xoy中,設(shè)點F(0, p)(p>0), 直線l : y= -p, 點P在直線l上移動,R是線段PF與x軸的交點, 過R、P分別作直線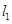 、
、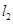 ,使
,使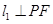 ,
,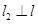
 .
.
(1) 求動點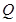 的軌跡
的軌跡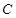 的方程;
的方程;
(2)在直線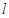 上任取一點
上任取一點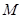 做曲線
做曲線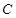 的兩條切線,設(shè)切點為
的兩條切線,設(shè)切點為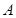 、
、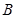 ,求證:直線
,求證:直線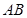 恒過一定點.
恒過一定點.
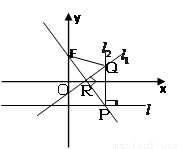
解:(1) 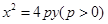 . (2)見解析.
. (2)見解析.
【解析】
試題分析:(Ⅰ)先判斷RQ是線段FP的垂直平分線,從而可得動點Q的軌跡C是以F為焦點,l為準(zhǔn)線的拋物線;
(Ⅱ)設(shè)M(m,-p),兩切點為A(x1,y1),B(x2,y2),求出切線方程,從而可得x1,x2為方程x2-2mx-4p2=0的兩根,進一步可得直線AB的方程,即可得到直線恒過定點(0,p);
解:(1)依題意知,點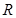 是線段
是線段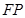 的中點,且
的中點,且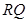 ⊥
⊥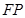 ,
,

∴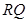 是線段
是線段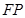 的垂直平分線. ∴
的垂直平分線. ∴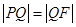 .
.
故動點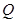 的軌跡
的軌跡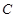 是以
是以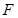 為焦點,
為焦點,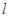 為準(zhǔn)線的拋物線,
為準(zhǔn)線的拋物線,
其方程為: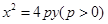 .
.
(2)設(shè)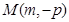 ,兩切點為
,兩切點為 ,
,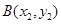
∴兩條切線方程為x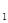 x=2p(y+y
x=2p(y+y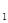 )
①
)
①
x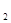 x=2p(y+y
x=2p(y+y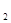 ) ②
) ②
對于方程①,代入點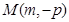 ,
又
,
又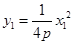 , 整理得:
, 整理得: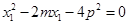 ,
同理對方程②有
,
同理對方程②有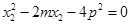 ,
即
,
即 為方程
為方程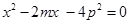 的兩根.
的兩根.
∴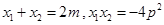 ③
③
設(shè)直線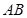 的斜率為
的斜率為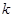 ,
,
所以直線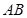 的方程為
的方程為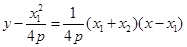 ,展開得:
,展開得: ,代入③得:
,代入③得: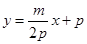 ,
∴直線恒過定點
,
∴直線恒過定點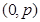 .
.
考點:本題主要考查了拋物線的定義,考查直線恒過定點,考查直線的向量,,屬于中檔題.
點評:解決該試題的關(guān)鍵是正確運用圓錐曲線的定義和韋達定理,來表示根與系數(shù)的關(guān)系的運用。


科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年廣東省肇慶市高三復(fù)習(xí)必修五綜合練習(xí) 題型:解答題
(本小題14分)如圖所示,L是海面上一條南北方向的海防警戒線,在L上點A處有一個水聲監(jiān)測點,另兩個監(jiān)測點B,C分別在A的正東方20 km處和54 km處.某時刻,監(jiān)測點B收到發(fā)自靜止目標(biāo)P的一個聲波,8s后監(jiān)測點A,20 s后監(jiān)測點C相繼收到這一信號.在當(dāng)時氣象條件下,聲波在水中的傳播速度是1. 5 km/s.
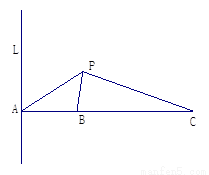
(1)設(shè)A到P的距離為 km,用
km,用 分別表示B、C到P 的距離,并求
分別表示B、C到P 的距離,并求 值;
值;
(2)求靜止目標(biāo)P到海防警戒線L的距離(結(jié)果精確到0.01 km)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年江蘇省高一上學(xué)期期末考試數(shù)學(xué)試卷 題型:解答題
(本小題14分)
如圖,已知 的面積為14,
的面積為14, 、
、 分別為邊
分別為邊 、
、 上的點,且
上的點,且


 ,
, 與
與 交于
交于 。設(shè)存在
。設(shè)存在 和
和 使
使 ,
, ,
, ,
, 。
。
(1)求 及
及
(2)用 ,
, 表示
表示
(3)求 的面積
的面積
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆廣東省高二上學(xué)期期末考試?yán)砜茢?shù)學(xué)試卷 題型:解答題
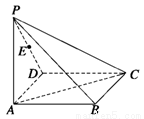
(本小題14分)如圖所示,在四棱錐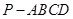 中,底面
中,底面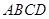 為矩形,側(cè)棱
為矩形,側(cè)棱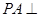 底面
底面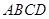 ,
, 為
為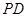 的中點.
的中點.
(1)求直線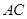 與
與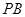 所成角的余弦值;
所成角的余弦值;
(2)在側(cè)面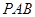 內(nèi)找一點
內(nèi)找一點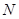 ,使
,使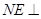 平面
平面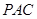 ,并分別求出點
,并分別求出點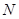 到
到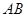 和
和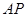 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:寧波市2010屆高三三模考試文科數(shù)學(xué)試題 題型:解答題
(本小題14分)如圖,三棱錐 中,
中, 平面
平面 ,
,
 ,
, ,
, 分別是
分別是 上
上
的動點,且 平面
平面 ,二面角
,二面角 為
為 .
.
(1)求證: 平面
平面 ;
;
(2)若 ,求直線
,求直線 與平面
與平面 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年江蘇省揚州市高三第四次模擬考試數(shù)學(xué)試題 題型:解答題
(本小題14分)
如圖,在直三棱柱 中,
中, ,點
,點 在邊
在邊 上,
上, 。
。
(1)求證: 平面
平面 ;
;
(2)如果點 是
是 的中點,求證:
的中點,求證: 平面
平面 .
.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com