思路解析：（1）要求k的值，必須建立關于k的方程，由已知OA⊥OB，所以kOA·kOB=-1，及A、B既在直線上，又在雙曲線上可得k的值.（2）為開放性題目，一般方法為：假設存在，根據已知求解，若解出而且符合題意則存在，若無解或解出不符合題意，則不存在.
解：（1）設A（x1,kx1+1）,B(x2,kx2+1)，則以AB為直徑的圓過原點的充要條件是（
）·（
）=-1,
即(k2+1)x1x2+k(x1+x2)+1=0. ①
由方程組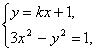
消去y,得（3-k2）x2-2kx-2=0. ②
∴x1+x2=
,x1x2=
，代入①得
+
+1=0,
解得k2=1,∴k=1或k=-1,當k=1時，方程②為2x2-2x-2=0,有兩個不等實根；當k=-1時，方程②為x2+x-1=0,有兩個不等實根,故k=±1時，以AB為直徑的圓過原點.
（2）若A（x1，kx1+1）,B(x2,kx2+1)關于y=2x對稱，
則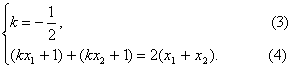
④整理得(k-2)(x1+x2)+2=0.
∵x1+x2=
,∴
+2=0,解得k=
.
這個結果與③矛盾，故不存在k的值，使A、B兩點關于直線y=2x對稱.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
| x2 |
| 2 |
| y2 |
| m |
| A、（1，2] |
| B、[1，2） |
| C、[1，2）∪[2，+∞） |
| D、（2，+∞） |
查看答案和解析>>
科目：高中數學 來源： 題型：
查看答案和解析>>
科目：高中數學 來源： 題型：
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
4
| ||
| 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com