
【題目】己知函數![]() .
.
(1)若f(x)有兩個極值點,求實數m的取值范圍:
(2)若函數![]() 有且只有三個不同的零點,分別記為x1,x2,x3,設x1<x2<x3,且
有且只有三個不同的零點,分別記為x1,x2,x3,設x1<x2<x3,且![]() 的最大值是e2,求x1x3的最大值.
的最大值是e2,求x1x3的最大值.
【答案】(1) (0,![]() );(2)
);(2)![]() .
.
【解析】
(1)求出函數的導數,利用函數f(x)有兩個極值點,說明導函數有兩個解,即![]() 有兩個不等的實數根,令
有兩個不等的實數根,令![]() ,則
,則![]() ,求得
,求得![]() 的極大值
的極大值![]() ,可求得m的取值范圍.
,可求得m的取值范圍.
(2)根據g(x) =(x-e)(lnx-mx),得到x=e是其零點.又結合(1)知lnx-mx=0的兩個根分別在(0,e),(e,+∞)上,得到g(x)的三個不同的零點分別是x1,e,x3,且0<x1<e,x3>e,進行![]() 的換元,則t∈
的換元,則t∈![]() .由
.由 ,解得
,解得 構造
構造![]() ,t∈
,t∈![]() ,利用導函數轉化求解即可.
,利用導函數轉化求解即可.
(1)由題意得![]() ,x>0.
,x>0.
由題知![]() =0有兩個不等的實數根,
=0有兩個不等的實數根,
即![]() 有兩個不等的實數根.令
有兩個不等的實數根.令![]() ,則
,則![]() .
.
由![]() >0,解得
>0,解得![]() ,故
,故![]() 在(0,e)上單調遞增;
在(0,e)上單調遞增;
由![]() <0,解得x>e,故
<0,解得x>e,故![]() 在(e,+∞)上單調遞減;
在(e,+∞)上單調遞減;
故![]() 在x=e處取得極大值
在x=e處取得極大值![]() ,且
,且![]() ,
,
結合圖形可得![]() .
.
∴當函數f(x)有兩個極值點時,實數m的取值范圍是(0,![]() ).
).
(2)因為g(x)=xlnx-mx2-elnx+mex=(x-e)(lnx-mx),
顯然x=e是其零點.
由(1)知lnx-mx=0的兩個根分別在(0,e),(e,+∞)上,
∴ g(x)的三個不同的零點分別是x1,e,x3,且0<x1<e,x3>e.
令![]() ,則t∈
,則t∈![]() .
.
則由 解得
解得
故![]() ,t∈
,t∈![]() .
.
令![]() ,則
,則![]() .
.
令![]() ,則
,則![]() .
.
所以![]() 在區間
在區間![]() 上單調遞增,即
上單調遞增,即![]() >
>![]() .所以
.所以![]() ,即
,即![]() 在區間
在區間![]() 上單調遞增,即
上單調遞增,即![]() ≤
≤![]() =
=![]() ,所以
,所以![]() ,即x1x3≤
,即x1x3≤![]() .
.
所以x1x3的最大值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知直線![]() ,閱讀如圖所示的程序框圖,若輸入的
,閱讀如圖所示的程序框圖,若輸入的![]() 的值為
的值為![]() ,輸出的
,輸出的![]() 的值恰為直線
的值恰為直線![]() 在
在![]() 軸上的截距,且
軸上的截距,且![]() .
.

(1)求直線![]() 與
與![]() 的交點坐標;
的交點坐標;
(2)若直線![]() 過直線
過直線![]() 與
與![]() 的交點,且在
的交點,且在![]() 軸上的截距是在
軸上的截距是在![]() 軸上的截距的2倍,求
軸上的截距的2倍,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x﹣1)|x﹣a|﹣x﹣2a(x∈R).
(1)若a=﹣1,求方程f(x)=1的解集;
(2)若![]() ,試判斷函數y=f(x)在R上的零點個數.
,試判斷函數y=f(x)在R上的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】進入冬天,大氣流動性變差,容易形成霧握天氣,從而影響空氣質量.某城市環保部門試圖探究車流量與空氣質量的相關性,以確定是否對車輛實施限行.為此,環保部門采集到該城市過去一周內某時段車流量與空氣質量指數的數據如下表:

(1)根據表中周一到周五的數據,求y關于x的線性回歸方程。
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2,則認為得到的線性回歸方程是可靠的.請根據周六和周日數據,判定所得的線性回歸方程是否可靠?
注:回歸方程![]() 中斜率和截距最小二乘估計公式分別為
中斜率和截距最小二乘估計公式分別為 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABC﹣A1B1C1,中,點M是棱BC的中點.
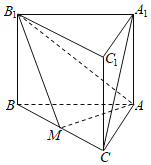
(2)求證:A1C∥平面AB1M;
(2)如果AB=AC,求證AM⊥平面BCC1B1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知斜率為1的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且線段
兩點,且線段![]() 的中點為
的中點為![]() ,橢圓
,橢圓![]() 的上頂點為
的上頂點為![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,若直線
兩點,若直線![]() 與
與![]() 的斜率之和為2,證明:
的斜率之和為2,證明:![]() 過定點.
過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com