若函數f(x)滿足:在定義域內存在實數x,使f(x+k)=f(x)+f(k)(k為常數),則稱“f(x)關于k可線性分解”
(1)函數f(x)=2x+x2是否關于1可線性分解?請說明理由;
(2)已知函數g(x)=lnx-ax+1(a>0)關于a可線性分解,求a的范圍;
(3)在(2)的條件下,當a取最小整數時,求g(x)的單調區間.
【答案】
分析:(1)函數f(x)=2
x+x
2關于1可線性分解.理由如下:令h(x)=f(x+1)-f(x)-f(1)=2(2
x-1+x-1),h(0)=-1,h(1)=2.
由零點存在定理可得:存在零點x
∈(0,1),使得h(x
)=0,即f(x
+1)=f(x
)+f(1).
(2)由題意,存在x
,使g(x
+a)=g(x
)+g(a),化為ln(x
+a)=lnx
+lna+1,即
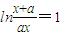
,
可得
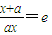
,利用x
>0及a>0,即可解得a的取值范圍.
(3)由(2)可知:a=1,可得g(x)=lnx-x+1.
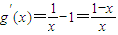
.分別解出g′(x)<0與g′(x)>0的x的取值范圍即可得出其單調區間.
解答:解:(1)函數f(x)=2
x+x
2關于1可線性分解.理由如下:
令h(x)=f(x+1)-f(x)-f(1)=2
x+1+(x+1)
2-2
x-x
2-2-1,
化為h(x)=2(2
x-1+x-1),h(0)=-1,h(1)=2,
∴存在零點x
∈(0,1),使得h(x
)=0,即f(x
+1)=f(x
)+f(1).
(2)由題意,存在x
,使g(x
+a)=g(x
)+g(a),
即ln(x
+a)-a(x
+a)+1=
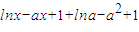
,
化為ln(x
+a)=lnx
+lna+1,即
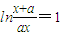
,
∴
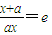
,解得

,
由a>0,得
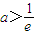
.
(3)由(2)可知:a=1,可得g(x)=lnx-x+1.

.
當x∈(0,1)時,g′(x)>0,∴g(x)的單調遞增區間是(0,1);
當x∈(1,+∞)時,g′(x)<0,∴g(x)的單調遞減區間是(1,+∞).
點評:正確理解“f(x)關于k可線性分解”的意義,熟練掌握利用導數研究函數的單調性的方法、零點存在定理、對數的運算法則等是解題的關鍵.

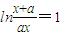 ,
,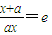 ,利用x>0及a>0,即可解得a的取值范圍.
,利用x>0及a>0,即可解得a的取值范圍.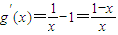 .分別解出g′(x)<0與g′(x)>0的x的取值范圍即可得出其單調區間.
.分別解出g′(x)<0與g′(x)>0的x的取值范圍即可得出其單調區間.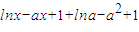 ,
,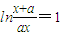 ,
,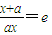 ,解得
,解得 ,
,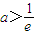 .
. .
.
