
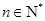 ,
,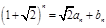 (
(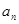 、
、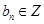 ).
).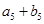 的值; (2)求證:數(shù)列
的值; (2)求證:數(shù)列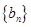 各項均為奇數(shù).
各項均為奇數(shù).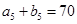 .(2)略
.(2)略 時,
時,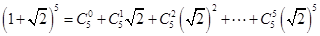
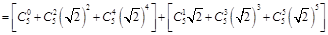
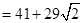
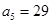 ,
,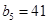 ,所以
,所以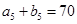 .
. 時,易知
時,易知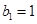 ,為奇數(shù);
,為奇數(shù);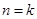 時,
時,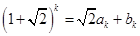 ,其中
,其中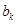 為奇數(shù);
為奇數(shù);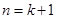 時,
時,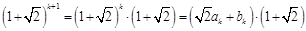
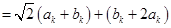
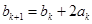 ,又
,又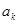 、
、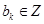 ,所以
,所以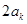 是偶數(shù),
是偶數(shù),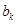 是奇數(shù),故
是奇數(shù),故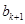 也是奇數(shù).
也是奇數(shù).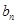 的值一定是奇數(shù).
的值一定是奇數(shù).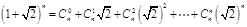
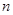 為奇數(shù)時,
為奇數(shù)時,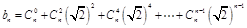
 時,
時,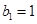 是奇數(shù);當(dāng)
是奇數(shù);當(dāng)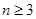 時,
時,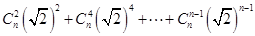 中必能被2整除,所以為偶數(shù),
中必能被2整除,所以為偶數(shù),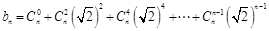 必為奇數(shù);
必為奇數(shù);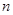 為偶數(shù)時,
為偶數(shù)時,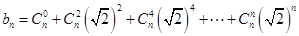
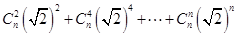 均能被2整除,于是
均能被2整除,于是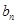 必為奇數(shù).綜上可知,
必為奇數(shù).綜上可知,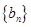 各項均為奇數(shù)
各項均為奇數(shù)

科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
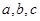 ,且A,B,C成等差數(shù)列,
,且A,B,C成等差數(shù)列,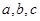 也成等差數(shù)列,求證ΔABC為等邊三角形.
也成等差數(shù)列,求證ΔABC為等邊三角形.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
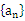 的首項
的首項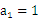 ,公差
,公差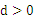 ,且第2項、第5項、第14項分別是等比數(shù)列
,且第2項、第5項、第14項分別是等比數(shù)列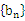 的第2項、第3項、第4項。
的第2項、第3項、第4項。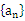 與
與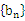 的通項公式;
的通項公式;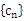 對
對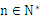 均有
均有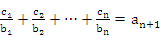 成立,求
成立,求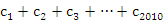 +
+ 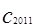
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
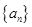 中,已知
中,已知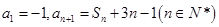 。
。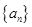 的通項公式;
的通項公式;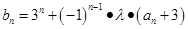 (
(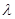 為非零常數(shù)),問是否存在整數(shù)
為非零常數(shù)),問是否存在整數(shù)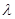 ,使得對任意的
,使得對任意的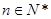 都有
都有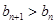 ?若存在,求出
?若存在,求出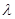 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com