
【題目】某種設備隨著使用年限的增加,每年的維護費相應增加.現對一批該設備進行調查,得到這批設備自購入使用之日起,前5年平均每臺設備每年的維護費用大致如表:
年份 |
|
|
|
|
|
維護費 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)從這![]() 年中隨機抽取兩年,求平均每臺設備每年的維護費用至少有
年中隨機抽取兩年,求平均每臺設備每年的維護費用至少有![]() 年多于
年多于![]() 萬元的概率;
萬元的概率;
(Ⅲ)求![]() 關于
關于![]() 的線性回歸方程;并據此預測第幾年開始平均每臺設備每年的維護費用超過
的線性回歸方程;并據此預測第幾年開始平均每臺設備每年的維護費用超過![]() 萬元.
萬元.
參考公式:用最小二乘法求線性回歸方程![]() 的系數公式:
的系數公式:
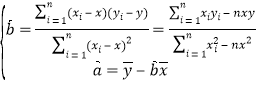
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 第10年開始平均每臺設備每年的維護費用超過5萬元.
第10年開始平均每臺設備每年的維護費用超過5萬元.
【解析】
(I)直接利用![]() ,用平均數的公式求解即可;
,用平均數的公式求解即可;
(II)分別求出維護費用不超過2萬元的有3年,分別編號為![]() ;超過2萬元的有2年,編號為
;超過2萬元的有2年,編號為![]() ,然后列出隨機抽取兩年的總事件,找出符合題意的,求的概率;
,然后列出隨機抽取兩年的總事件,找出符合題意的,求的概率;
(Ⅲ)先求出![]() ,
,![]() ,
,![]() ,然后利用公式求得回歸方程
,然后利用公式求得回歸方程![]() ,再根據題意解得維護費用超過
,再根據題意解得維護費用超過![]() 萬元,得出答案.
萬元,得出答案.
解:(Ⅰ)由![]() .
.
(Ⅱ)5年中平均每臺設備每年的維護費用不超過2萬元的有3年,分別編號為![]() ;超過2萬元的有2年,編號為
;超過2萬元的有2年,編號為![]() .隨機抽取兩年,基本事件為
.隨機抽取兩年,基本事件為![]() ,
,![]() ,
,![]() ,
,![]() 共10個,而且這些基本事件的出現是等可能的.
共10個,而且這些基本事件的出現是等可能的.
用![]() 表示“抽取的2年中平均每臺設備每年的維護費用至少有1年多于2萬元”,則
表示“抽取的2年中平均每臺設備每年的維護費用至少有1年多于2萬元”,則![]() 包含的基本事件有
包含的基本事件有![]() 共7個,故
共7個,故![]() .
.
(Ⅲ)![]() ,
,![]() ,
,![]()
![]() ,
,![]()
∴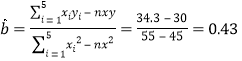 ,
,![]()
所以回歸方程為![]() .
.
由題意有![]() ,
,
故第10年開始平均每臺設備每年的維護費用超過5萬元


科目:高中數學 來源: 題型:
【題目】為調查某社區居民的業余生活狀況,研究這一社區居民在20:00-22:00時間段的休閑方式與性別的關系,隨機調查了該社區80人,得到下面的數據表:
休閑方式 性別 | 看電視 | 看書 | 合計 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合計 | 20 | 60 | 80 |
(1)根據以上數據,能否有![]() 的把握認為“在20:00-22:00時間段的休閑方式與性別有關系”?
的把握認為“在20:00-22:00時間段的休閑方式與性別有關系”?
(2)將此樣本的頻率估計為總體的概率,隨機調查3名在該社區的男性,設調查的3人在這一時間段以看書為休閑方式的人數為隨機變量![]() ,求
,求![]() 的數學期望和方差.
的數學期望和方差.
參考公式與數據![]() 對應
對應![]() ,
,![]() 對應
對應![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
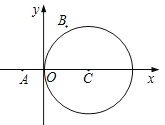
【題目】如圖,在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 及點
及點![]() ,
,![]() .
.
(1)若直線![]() 平行于
平行于![]() ,與圓
,與圓![]() 相交于
相交于![]() ,
,![]() 兩點,
兩點,![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)在圓![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,求點
?若存在,求點![]() 的個數;若不存在,說明理由.
的個數;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 的動直線
的動直線![]() 與橢圓相交于
與橢圓相交于![]() ,
,![]() 兩點,當直線
兩點,當直線![]() 平行
平行![]() 軸時,直線
軸時,直線![]() 被橢圓
被橢圓![]() 截得的線段長為4.
截得的線段長為4.

(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 為坐標原點,是否存在常數
為坐標原點,是否存在常數![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() (
(![]() ,且
,且![]() ).
).
(1)當![]() (其中
(其中![]() ,且t為常數)時,
,且t為常數)時,![]() 是否存在最小值,如果存在,求出最小值;如果不存在,請說明理由;
是否存在最小值,如果存在,求出最小值;如果不存在,請說明理由;
(2)當![]() 時,求滿足不等式
時,求滿足不等式![]() 的實數x的取值范圍.
的實數x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com