如果二次函數y=x2-(a-1)x+5在(0,1)是增函數,那么f(2)的取值范圍是 .
【答案】
分析:求出二次函數f(x)=x
2-(a-1)x+5的對稱軸,根據題意求出a的范圍,再利用不等式的性質即可求出f(2)的取值范圍.
解答:解:二次函數f(x)=x
2-(a-1)x+5的對稱軸為x=
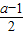
,開口向上,
又二次函數f(x)在區間(0,1)上為增函數,
則
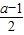
≤0,解得a≤1,
f(2)=4-2(a-1)+5=9-2(a-1)=11-2a,11-2a≥11-2=9,
故f(2)的取值范圍是[9,+∞).
故答案為:[9,+∞).
點評:此題主要考查二次函數的單調性、函數值的求解及不等式的性質,屬中檔題.
