
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 1 |
| 8 |
| C | 03 |
| 9 |
| 3 |
| 1 |
| 97 |
| C | 13 |
| 9 |
| 3 |
| 9 |
| 3 |
| 9 |
| 9 |
| C | 93 |
| 9 |
| 3 |
| 9 |
| 3 |
| 3 |
| 9 |
| C | 33 |
| 9 |
| 3 |
| 8 |
| 97 |
| 1 |
| 97 |
| 9 |
| 9 |
| 3 |
| 9 |
| 8 |
| 97 |
| 9 |
| 3 |
| C | k3 |
| 9 |
| 3 |
| 9 |
| 3 |
| C | k3 |
| 9k |
| 33 |
| 9 |
| 3 |
| 9 |
| 3 |
| C | 93 |
| 9 |
| 3 |
| 9 |
| 3 |
| 9 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 9 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 10 |
| 33 |
| C | 33 |
| 9 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 3 |
| 3v |
| 10 |
| 33 |
| 3 |
| 3v |
| 33 |
| 3v |
| 33 |
| 933 |
| 9 |
| 3 |
| 1 |
| 39 |
| 1 |
| 9 |
| C | 93 |
| 99 |
| 39 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 39 |
| 1 |
| 9 |
| C | 19 |
| 9 |
| 39 |
| 33 |
| 933 |


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2013屆廣東惠陽一中實驗學校高二6月月考理科數學試卷(解析版) 題型:解答題
(本題滿分12分)
甲、乙兩隊參加奧運知識競賽,每隊3人,每人回答一個問題,答對者為本隊贏得一分,
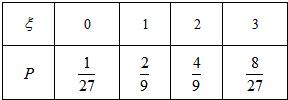
答錯得零分.假設甲隊中每人答對的概率均為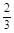 ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為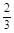 ,
,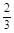 ,
, ,且各人回答正確與否相互之間沒有影響.用
,且各人回答正確與否相互之間沒有影響.用 表示甲隊的總得分.
表示甲隊的總得分.
(1)求 的概率及
的概率及 的數學期望
的數學期望 ;
;
(2)用A表示“甲、乙兩個隊總得分之和等于3”這一事件,用B表示“甲隊總得分大于乙隊總得分”這一事件,求 .
.
查看答案和解析>>
科目:高中數學 來源:2009-2010學年浙江省溫州市八校聯考高三(上)入學數學試卷(理科)(解析版) 題型:解答題
 ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為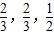 ,且各人回答正確與否相互之間沒有影響.用ξ表示甲隊的總得分.
,且各人回答正確與否相互之間沒有影響.用ξ表示甲隊的總得分.查看答案和解析>>
科目:高中數學 來源:2012年江西省鷹潭一中高考數學模擬試卷(文科)(解析版) 題型:解答題
 ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為 ,且各人回答正確與否相互之間沒有影響.用ξ表示甲隊的總得分.
,且各人回答正確與否相互之間沒有影響.用ξ表示甲隊的總得分.查看答案和解析>>
科目:高中數學 來源:2008年山東省高考數學試卷(理科)(解析版) 題型:解答題
 ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為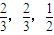 ,且各人回答正確與否相互之間沒有影響.用ξ表示甲隊的總得分.
,且各人回答正確與否相互之間沒有影響.用ξ表示甲隊的總得分.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com