
【題目】已知圓![]()
![]() ,點
,點![]() ,以線段
,以線段![]() 為直徑的圓內切于圓
為直徑的圓內切于圓![]() ,記點
,記點![]() 的軌跡為
的軌跡為![]() .
.
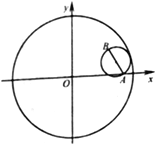
(1)求曲線![]() 的方程;
的方程;
(2)直線![]() 交圓
交圓![]() 于
于![]() ,
,![]() 兩點,當
兩點,當![]() 為
為![]() 的中點時,求直線
的中點時,求直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
試題本題主要考查橢圓的標準方程和幾何性質、直線的標準方程和幾何性質等基礎知識,意在考查考生的分析問題解決問題的能力、讀圖能力、運算求解能力. 第一問,設AB的中點為M,切點為N,連OM,MN,先利用半徑長得出|OM|+|MN|=2,再利用中位線轉化邊,得|AB|+|AB|=2(|OM|+|MN|)=4,得到橢圓的定義,從而得到a,b,c的值,寫出橢圓的方程;第二問,利用OB⊥CD,利用向量垂直的充要條件,得到坐標關系,再結合橢圓方程,可解出![]() ,從而得到直線AB的斜率,得到直線AB的方程.
,從而得到直線AB的斜率,得到直線AB的方程.
試題解析:(Ⅰ)設AB的中點為M,切點為N,連OM,MN,則
|OM|+|MN|=|ON|=2,取A關于y軸的對稱點A,
連AB,故|AB|+|AB|=2(|OM|+|MN|)=4.
所以點B的軌跡是以A,A為焦點,長軸長為4的橢圓.
其中,a=2,![]() ,b=1,則
,b=1,則
曲線Γ的方程為![]() . 5分
. 5分
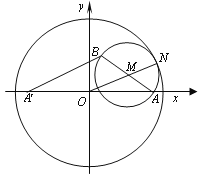
(Ⅱ)因為B為CD的中點,所以OB⊥CD,
則![]() .設B(x0,y0),
.設B(x0,y0),
則![]() . 7分
. 7分
又![]() 解得
解得![]() ,
,![]() .
.
則kOB=![]() ,kAB=
,kAB=![]()
![]() , 10分
, 10分
則直線AB的方程為![]() ,即
,即
![]() 或
或![]() . 12分
. 12分


科目:高中數學 來源: 題型:
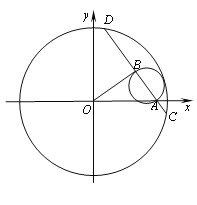
【題目】如圖所示,在平面直角坐標系![]() 中,平行于
中,平行于![]() 軸且過點
軸且過點![]() 的入射光線
的入射光線![]() 被直線
被直線![]() 反射,反射光線
反射,反射光線![]() 交
交![]() 軸于
軸于![]() 點,圓
點,圓![]() 過點
過點![]() ,且與
,且與![]() 、
、![]() 相切.
相切.
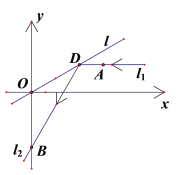
(Ⅰ)求![]() 所在直線的方程;
所在直線的方程;
(Ⅱ)求圓![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某射擊運動員進行射擊訓練,前三次射擊在靶上的著彈點![]() 剛好是邊長為
剛好是邊長為![]() 的等邊三角形的三個頂點.
的等邊三角形的三個頂點.

(Ⅰ)第四次射擊時,該運動員瞄準![]() 區域射擊(不會打到
區域射擊(不會打到![]() 外),則此次射擊的著彈點距
外),則此次射擊的著彈點距![]() 的距離都超過
的距離都超過![]() 的概率為多少?(彈孔大小忽略不計)
的概率為多少?(彈孔大小忽略不計)
(Ⅱ) 該運動員前三次射擊的成績(環數)都在區間![]() 內,調整一下后,又連打三槍,其成績(環數)都在區間
內,調整一下后,又連打三槍,其成績(環數)都在區間![]() 內.現從這
內.現從這![]() 次射擊成績中隨機抽取兩次射擊的成績(記為
次射擊成績中隨機抽取兩次射擊的成績(記為![]() 和
和![]() )進行技術分析.求事件“
)進行技術分析.求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,根據經驗,其次品率![]() 與日產量
與日產量![]() (萬件)之間滿足關系,
(萬件)之間滿足關系, (其中
(其中![]() 為常數,且
為常數,且![]() ,已知每生產1萬件合格的產品以盈利2萬元,但每生產1萬件次品將虧損1萬元(注:次品率=次品數/生產量, 如
,已知每生產1萬件合格的產品以盈利2萬元,但每生產1萬件次品將虧損1萬元(注:次品率=次品數/生產量, 如![]() 表示每生產10件產品,有1件次品,其余為合格品).
表示每生產10件產品,有1件次品,其余為合格品).
(1)試將生產這種產品每天的盈利額![]() (萬元)表示為日產量
(萬元)表示為日產量![]() (萬件)的函數;
(萬件)的函數;
(2)當日產量為多少時,可獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國城市空氣污染指數范圍及相應的空氣質量類別見下表:
空氣污染指數 | 空氣質量 | 空氣污染指數 | 空氣質量 | |
0--50 | 優 | 201--250 | 中度污染 | |
51--100 | 良 | 251--300 | 中度重污染 | |
101--150 | 輕微污染 | >300 | 重污染 | |
151----200 | 輕度污染 |
我們把某天的空氣污染指數在0-100時稱作A類天,101--200時稱作B類天,大于200時稱作C類天.下圖是某市2014年全年監測數據中隨機抽取的18天數據作為樣本,其莖葉圖如下:(百位為莖,十.個位為葉)

(1)從這18天中任取3天,求至少含2個A類天的概率;
(2)從這18天中任取3天,記X是達到A類或B類天的天數,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在D上的函數f(x),如果滿足對任意x∈D,存在常數M>0,都有|f(x)|≤M成立,則稱f(x)是D上的有界函數,其中M稱為函數f(x)的上界,已知函數f(x)=1+x+ax2
(1)當a=﹣1時,求函數f(x)在(﹣∞,0)上的值域,判斷函數f(x)在(﹣∞,0)上是否為有界函數,并說明理由;
(2)若函數f(x)在x∈[1,4]上是以3為上界的有界函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為提高員工的綜合素質,聘請專業機構對員工進行專業技術培訓,其中培訓機構費用成本為12000元.公司每位員工的培訓費用按以下方式與該機構結算:若公司參加培訓的員工人數不超過30人時,每人的培訓費用為850元;若公司參加培訓的員工人數多于30人,則給予優惠:每多一人,培訓費減少10元.已知該公司最多有60位員工可參加培訓,設參加培訓的員工人數為![]() 人,每位員工的培訓費為
人,每位員工的培訓費為![]() 元,培訓機構的利潤為
元,培訓機構的利潤為![]() 元.
元.
(1)寫出![]() 與
與![]()
![]() 之間的函數關系式;
之間的函數關系式;
(2)當公司參加培訓的員工為多少人時,培訓機構可獲得最大利潤?并求最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() ,點
,點![]() 是橢圓
是橢圓![]() 內且在
內且在![]() 軸上的一個動點,過點
軸上的一個動點,過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點(
兩點(![]() 在第一象限),且
在第一象限),且![]() .
.
(Ⅰ)若點![]() 為橢圓
為橢圓![]() 的下頂點,求點
的下頂點,求點![]() 的坐標;
的坐標;
(Ⅱ)當![]() (
(![]() 為坐標原點)的面積最大時,求點
為坐標原點)的面積最大時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com