解:(Ⅰ)當a=1時,f(x)=x
2-e
x,f(x)在R上單調遞減.
事實上,要證f
′(x)=x
2-e
x在R上為減函數,只要證明f
′(x)≤0對?x∈R恒成立即可,
設g(x)=f
′(x)=2x-e
x,則g
′(x)=2-e
x,
當x=ln2時,g
′(x)=0,
當x∈(-∞,ln2)時,g
′(x)>0,當x∈(ln2,+∞)時,g
′(x)<0.
∴函數g(x)在(-∞,ln2)上為增函數,在(ln2,+∞)上為減函數.
∴f
′(x)
max=g(x)
max=g(ln2)=2ln2-2<0,故f
′(x)<0恒成立
所以f(x)在R上單調遞減;
(Ⅱ)(i)由f(x)=ax
2-e
x,所以,f
′(x)=2ax-e
x.
若f(x)有兩個極值點x
1,x
2,則x
1,x
2是方程f
′(x)=0的兩個根,
故方程2ax-e
x=0有兩個根x
1,x
2,
又因為x=0顯然不是該方程的根,所以方程
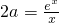
有兩個根,
設
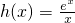
,得
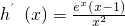
.
若x<0時,h(x)<0且h
′(x)<0,h(x)單調遞減.
若x>0時,h(x)>0.
當0<x<1時h
′(x)<0,h(x)單調遞減,
當x>1時h
′(x)>0,h(x)單調遞增.
要使方程
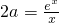
有兩個根,需2a>h(1)=e,故

且0<x
1<1<x
2.
故a的取值范圍為
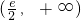
.
(ii)證明:由f
′(x
1)=0,得:
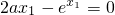
,故
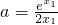
,x
1∈(0,1)
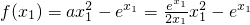
=
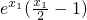
,x
1∈(0,1)
設s(t)=
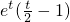
(0<t<1),則
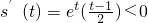
,s(t)在(0,1)上單調遞減
故s(1)<s(t)<s(0),即
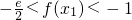
.
分析:(Ⅰ)把a=1代入函數解析式,求出函數的導函數,把導函數二次求導后,求出導函數的最大值,得到導函數的最大值小于0,從而得到原函數是實數集上的減函數;
(Ⅱ)(i)把函數f(x)=ax
2-e
x有兩個極值點轉化為其導函數f
′(x)=2ax-e
x有兩個根,分離變量a后分析右側函數
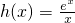
的單調性,該函數先減后增有極小值,然后根據圖象的交點情況得到a的范圍;
(ii)由x
1是原函數的導函數的根,把x
1代入導函數解析式,用x
1表示a,然后把f(x
1)的表達式中的a替換,得到關于x
1的函數式后再利用求導判斷單調性,從而得到要征得結論.
點評:本題考查了利用導數研究函數的單調性,考查了函數在某點取得極值的條件,解答此題的關鍵是利用二次求導判斷函數導函數的符號,這也是此類問題經常用到的方法.此題是有一定難度題目.

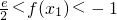 . (注:e是自然對數的底數)
. (注:e是自然對數的底數)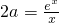 有兩個根,
有兩個根,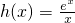 ,得
,得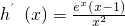 .
.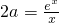 有兩個根,需2a>h(1)=e,故
有兩個根,需2a>h(1)=e,故 且0<x1<1<x2.
且0<x1<1<x2.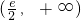 .
.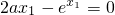 ,故
,故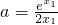 ,x1∈(0,1)
,x1∈(0,1)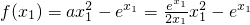 =
=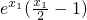 ,x1∈(0,1)
,x1∈(0,1)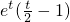 (0<t<1),則
(0<t<1),則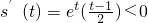 ,s(t)在(0,1)上單調遞減
,s(t)在(0,1)上單調遞減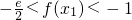 .
.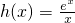 的單調性,該函數先減后增有極小值,然后根據圖象的交點情況得到a的范圍;
的單調性,該函數先減后增有極小值,然后根據圖象的交點情況得到a的范圍;
