(1)
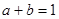
,所以
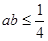
,所以
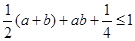
,
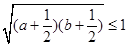
,從而有2+
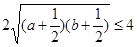
,即:
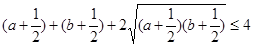
,所以原不等式成立 (2)8
試題分析:(1)證明:因為
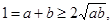
所以
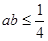
,所以
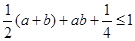
所以
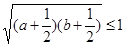
,從而有2+
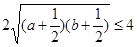
即:
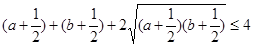
即:
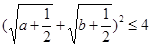
,所以原不等式成立.
(2)
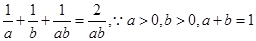
……2分

即
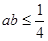
當且僅當
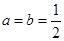
時等號成立
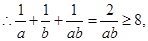
即當
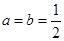
時,
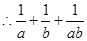
的最小值為8. 2分
點評:由均值不等式
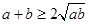
求最值時要滿足一正二定三相等,一,
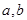
都是正實數(shù),二,當和為定值時,積取最值,當積為定值時,和為定值,三,當且僅當
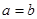
時等號成立取得最值
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
若實數(shù)
a、
b滿足
a+
b=2,是
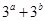
的最小值是( )
| A.18 | B.6 | C.2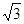 | D.2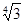 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若對于使

成立的所有常數(shù)

中,我們把

的最小值

叫做

的上確界,若

,則

的上確界是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
觀察下列兩個結(jié)論:
(Ⅰ)若
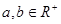
,且
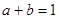
,則
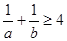
;
(Ⅱ)若
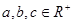
,且
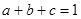
,則
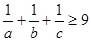
;
先證明結(jié)論(Ⅱ),再類比(Ⅰ)(Ⅱ)結(jié)論,請你寫出一個關(guān)于
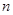
個正數(shù)
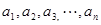
的結(jié)論?(寫出結(jié)論,不必證明。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設
x,
y>0,且
x+2
y=2,則
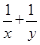
的最小值為
。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分10分)選修4 - 5 :不等式選講
設函數(shù),
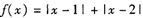
.
(I)求證
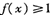
;
(II)若
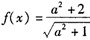
成立,求x的取值范圍.
查看答案和解析>>

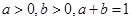 ,
,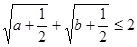 ; (2)求
; (2)求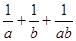 的最小值.
的最小值. 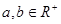 ,且
,且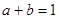 ,則
,則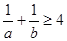 ;
;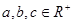 ,且
,且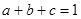 ,則
,則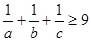 ;
;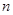 個正數(shù)
個正數(shù)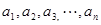 的結(jié)論?(寫出結(jié)論,不必證明。
的結(jié)論?(寫出結(jié)論,不必證明。