
【題目】如圖,港口A在港口O的正東100海里處,在北偏東方向有條直線航道OD,航道和正東方向之間有一片以B為圓心,半徑為![]() 海里的圓形暗礁群(在這片海域行船有觸礁危險),其中OB=
海里的圓形暗礁群(在這片海域行船有觸礁危險),其中OB=![]() 海里,tan∠AOB=
海里,tan∠AOB=![]() ,cos∠AOD=
,cos∠AOD=![]() ,現一艘科考船以
,現一艘科考船以![]() 海里/小時的速度從O出發沿OD方向行駛,經過2個小時后,一艘快艇以50海里/小時的速度準備從港口A出發,并沿直線方向行駛與科考船恰好相遇.
海里/小時的速度從O出發沿OD方向行駛,經過2個小時后,一艘快艇以50海里/小時的速度準備從港口A出發,并沿直線方向行駛與科考船恰好相遇.
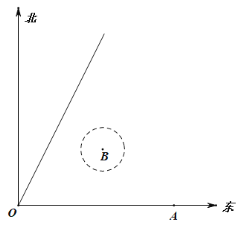
(1)若快艇立即出發,判斷快艇是否有觸礁的危險,并說明理由;
(2)在無觸礁危險的情況下,若快艇再等x小時出發,求x的最小值.
【答案】(1)快艇立即出發有觸礁的危險,見解析;(2)3-![]()
【解析】
(1) 以O為原點,正東方向為x軸,正北方向為y軸,建立直角坐標系xOy.再設設快艇立即出發經過t小時后兩船相遇于點C, 根據余弦定理可解得![]() ,繼而得出直線AC的方程,判斷出圓心到直線AC的距離小于半徑,即可知有危險.
,繼而得出直線AC的方程,判斷出圓心到直線AC的距離小于半徑,即可知有危險.
(2) 設快艇所走的直線![]() 與圓B相切,且與科考船相遇于點E.根據圓心B到直線AC的距離為
與圓B相切,且與科考船相遇于點E.根據圓心B到直線AC的距離為![]() 可求得直線OD的方程為y=2x.進而聯立方程可求得E(50,100),再計算兩船的時間差即可得x的最小值.
可求得直線OD的方程為y=2x.進而聯立方程可求得E(50,100),再計算兩船的時間差即可得x的最小值.
如圖,以O為原點,正東方向為x軸,正北方向為y軸,建立直角坐標系xOy.
因為OB=20![]() ,tan∠AOB=
,tan∠AOB=![]() ,OA=100,所以點B(60,40),且A(100,0).
,OA=100,所以點B(60,40),且A(100,0).
(1)設快艇立即出發經過t小時后兩船相遇于點C,則OC=10![]() (t+2),AC=50t.
(t+2),AC=50t.
因為OA=100,cos∠AOD=![]() ,所以AC2=OA2+OC2-2OA·OC·cos∠AOD,
,所以AC2=OA2+OC2-2OA·OC·cos∠AOD,
即(50t)2=1002+[10![]() (t+2)]2-2×100×10
(t+2)]2-2×100×10![]() (t+2)×
(t+2)×![]() .化得t2=4,解得t1=2,t2=-2(舍去),
.化得t2=4,解得t1=2,t2=-2(舍去),
所以OC=40![]() ,因為cos∠AOD=
,因為cos∠AOD=![]() ,所以sin∠AOD=
,所以sin∠AOD=![]() ,所以C(40,80),
,所以C(40,80),
所以直線AC的方程為y=-![]() (x-100),即4x+3y-400=0.
(x-100),即4x+3y-400=0.
因為圓心B到直線AC的距離d=![]() =8,而圓B的半徑r=8
=8,而圓B的半徑r=8![]() ,
,
所以d<r,此時直線AC與圓B相交,所以快艇有觸礁的危險.
答:若快艇立即出發有觸礁的危險.

(2)設快艇所走的直線![]() 與圓B相切,且與科考船相遇于點E.
與圓B相切,且與科考船相遇于點E.
設直線![]() 的方程為y=k(x-100),即kx-y-100k=0.
的方程為y=k(x-100),即kx-y-100k=0.
因為直線AE與圓B相切,所以圓心B到直線AC的距離d=![]() =
=![]() ,
,
即2k2+5k+2=0,解得k=-2或k=-![]() . 由(1)可知k=-
. 由(1)可知k=-![]() 舍去.
舍去.
因為cos∠AOD=![]() ,所以tan∠AOD=2,所以直線OD的方程為y=2x.
,所以tan∠AOD=2,所以直線OD的方程為y=2x.
由![]() 解得
解得![]() 所以E(50,100), 所以AE=50
所以E(50,100), 所以AE=50![]() ,OE=50
,OE=50![]() ,
,
此時兩船的時間差為![]() -
-![]() =5-
=5-![]() ,所以x≥5-
,所以x≥5-![]() -2=3-
-2=3-![]() .
.
x的最小值為![]() 小時.
小時.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() ).若
).若![]() ,
,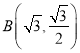 ,
,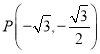 ,
,![]() 四點中有且僅有三點在橢面C上.
四點中有且僅有三點在橢面C上.
(1)求橢圓C的標準方程;
(2)設O為坐標原點,F為橢圓C的右焦點,過點F的直線l分別與橢圓C交于M,N兩點,![]() ,求證:直線
,求證:直線![]() ,
,![]() 關于x軸對稱.
關于x軸對稱.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,曲線
,曲線![]() 上任意一點到
上任意一點到![]() 的距離等于該點到直線
的距離等于該點到直線![]() 的距離.
的距離.
(Ⅰ)求![]() 及曲線
及曲線![]() 的方程;
的方程;
(Ⅱ)若直線![]() 與橢圓只有一個交點
與橢圓只有一個交點![]() ,與曲線
,與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() .過焦點且垂直于
.過焦點且垂直于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 相交所得的弦長為3,直線
相交所得的弦長為3,直線![]() 與橢圓
與橢圓![]() 相切.
相切.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() ,問直線
,問直線![]() 是否存在?若存在,求直線
是否存在?若存在,求直線![]() 的斜率
的斜率![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
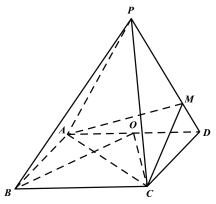
【題目】如圖,四棱錐P-ABCD的底面是平行四邊形,PD⊥AB,O是AD的中點,BO=CO.
(1)求證:AB⊥平面PAD;
(2)若AD=2AB=4, PA=PD,點M在側棱PD上,且PD=3MD,二面角P-BC-D的大小為![]() ,求直線BP與平面MAC所成角的正弦值.
,求直線BP與平面MAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】口袋中有大小、形狀、質地相同的兩個白球和三個黑球.現有一抽獎游戲規則如下:抽獎者每次有放回的從口袋中隨機取出一個球,最多取球2n+1(n![]() )次.若取出白球的累計次數達到n+1時,則終止取球且獲獎,其它情況均不獲獎.記獲獎概率為
)次.若取出白球的累計次數達到n+1時,則終止取球且獲獎,其它情況均不獲獎.記獲獎概率為![]() .
.
(1)求![]() ;
;
(2)證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,側棱
中,側棱![]() 底面
底面![]() ,底面三角形
,底面三角形![]() 是正三角形,E是BC中點,則下列敘述正確的是( )
是正三角形,E是BC中點,則下列敘述正確的是( )

A.![]() 與
與![]() 是異面直線B.
是異面直線B.![]() 平面
平面![]()
C.AE,![]() 為異面直線,且
為異面直線,且![]() D.
D.![]() 平面
平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春季,某出租汽車公同決定更換一批新的小汽車以代替原來報廢的出租車,現有采購成本分別為11萬元/輛和8萬元/輛的A,B兩款車型,根據以往這兩種出租車車型的數據,得到兩款出租車型使用壽命頻數表如表:
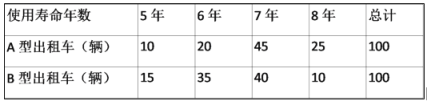
(1)填寫如表,并判斷是否有99%的把握認為出租車的使用壽命年數與汽車車有關?
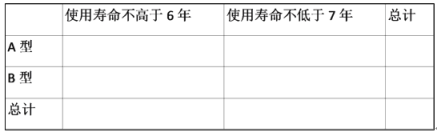
(2)以頻率估計概率,從2020年生產的A和B的車型中各隨機抽1車,以X表示這2車中使用壽命不低于7年的車數,求X的分布列和數學期望;
(3)根據公司要求,采購成本由出租公司負責,平均每輛出租每年上交公司6萬元,其余維修和保險等費用自理,假設每輛出租車的使用壽命都是整數年,用頻率估計每輛出租車使用壽命的概率,分別以這100輛出租車所產生的平均利潤作為決策依據,如果你是該公司的負責人,會選擇采購哪款車型?
參考公式: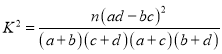 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
參考數據:
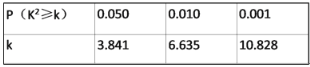
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且四個頂點構成的四邊形的面積是
,且四個頂點構成的四邊形的面積是![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 經過點
經過點![]() ,且不垂直于
,且不垂直于![]() 軸,直線
軸,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 為
為![]() 的中點,直線
的中點,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點(
兩點(![]() 是坐標原點),若四邊形
是坐標原點),若四邊形![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com