
(08年四川卷文)(本小題滿分12分)
如圖,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 與
與![]() 都是直角梯形,
都是直角梯形,
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() 分別為
分別為![]() 的中點(diǎn)
的中點(diǎn)
(Ⅰ)證明:四邊形![]() 是平行四邊形;
是平行四邊形;
(Ⅱ)![]() 四點(diǎn)是否共面?為什么?
四點(diǎn)是否共面?為什么?
(Ⅲ)設(shè)![]() ,證明:平面
,證明:平面![]() 平面
平面![]() ;
;
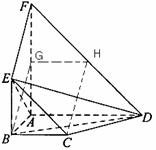
解法一:
(Ⅰ)由題意知,![]()
所以![]()
![]()
![]()
又![]()
![]()
![]() ,故
,故![]()
![]()
![]()
所以四邊形![]() 是平行四邊形。
是平行四邊形。

(Ⅱ)![]() 四點(diǎn)共面。理由如下:
四點(diǎn)共面。理由如下:
由![]()
![]()
![]() ,
,![]() 是
是![]() 的中點(diǎn)知,
的中點(diǎn)知,![]()
![]()
![]() ,所以
,所以![]()
由(Ⅰ)知![]() ,所以
,所以![]() ,故
,故![]() 共面。又點(diǎn)
共面。又點(diǎn)![]() 在直線
在直線![]() 上
上
所以![]() 四點(diǎn)共面。
四點(diǎn)共面。
(Ⅲ)連結(jié)![]() ,由
,由![]() ,
,![]()
![]()
![]() 及
及![]() 知
知![]() 是正方形
是正方形
故![]() 。由題設(shè)知
。由題設(shè)知![]() 兩兩垂直,故
兩兩垂直,故![]() 平面
平面![]() ,
,
因此![]() 是
是![]() 在平面
在平面![]() 內(nèi)的射影,根據(jù)三垂線定理,
內(nèi)的射影,根據(jù)三垂線定理,![]()
又![]() ,所以
,所以![]() 平面
平面![]()
由(Ⅰ)知![]() ,所以
,所以![]() 平面
平面![]() 。
。
由(Ⅱ)知![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,得平面
,得平面![]() 平面
平面![]()
解法二:
由平面![]() 平面
平面![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,以
,以![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),
射線![]() 為
為![]() 軸正半軸,建立如圖所示的直角坐標(biāo)系
軸正半軸,建立如圖所示的直角坐標(biāo)系![]()
(Ⅰ)設(shè)![]() ,則由題設(shè)得
,則由題設(shè)得
![]()
所以![]()
于是![]()
又點(diǎn)![]() 不在直線
不在直線![]() 上
上
所以四邊形![]() 是平行四邊形。
是平行四邊形。
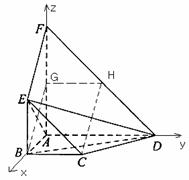
(Ⅱ)![]() 四點(diǎn)共面。理由如下:
四點(diǎn)共面。理由如下:
由題設(shè)知![]() ,所以
,所以
![]()
又![]() ,故
,故![]() 四點(diǎn)共面。
四點(diǎn)共面。
(Ⅲ)由![]() 得,所以
得,所以![]()
又![]() ,因此
,因此![]()
即![]()
又![]() ,所以
,所以![]() 平面
平面![]()
故由![]() 平面
平面![]() ,得平面
,得平面![]() 平面
平面![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(08年四川卷文)(本小題滿分12分)
如圖,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 與
與![]() 都是直角梯形,
都是直角梯形,
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() 分別為
分別為![]() 的中點(diǎn)
的中點(diǎn)
(Ⅰ)證明:四邊形![]() 是平行四邊形;
是平行四邊形;
(Ⅱ)![]() 四點(diǎn)是否共面?為什么?
四點(diǎn)是否共面?為什么?
(Ⅲ)設(shè)![]() ,證明:平面
,證明:平面![]() 平面
平面![]() ;
;

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(08年四川卷文)(本小題滿分12分)
設(shè)進(jìn)入某商場的每一位顧客購買甲種商品的概率為![]() ,購買乙種商品的概率為
,購買乙種商品的概率為![]() ,且購買甲種商品與購買乙種商品相互獨(dú)立,各顧客之間購買商品也是相互獨(dú)立的。
,且購買甲種商品與購買乙種商品相互獨(dú)立,各顧客之間購買商品也是相互獨(dú)立的。
(Ⅰ)求進(jìn)入商場的1位顧客購買甲、乙兩種商品中的一種的概率;
(Ⅱ)求進(jìn)入商場的3位顧客中至少有2位顧客既未購買甲種也未購買乙種商品的概率。
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com